之前的第一课里头提及了为什么 NLP 任务比较难，Deep Learning 在 NLP 领域中取得的成果也不如 CV 和 Speech 来得令人惊讶。

对于这个现象，有一种说法是：

语言（词、句子、篇章等）属于人类认知过程中产生的高层认知抽象实体，而语音和图像属于较为底层的原始输入信号，所以后两者更适合做deep learning来学习特征。

这里就涉及了深度学习中输入的问题，也是所有 NLP 任务中都无法绕过的问题，即在计算机里如何表示一个词？

答案显而易见，就是本节课的主题词向量 (Word Vector)。为了方便理解，我补充了一些课程中没有讲到的内容。

如何表示词的意思

姑且先看看 Webster 词典中对于 meaning 的定义：

1. the idea that is represented by a word, phrase, etc.
2. the idea that a person wants to express by using words, signs, etc.
3. the idea that is expressed in a word of writing, art, etc.

而在语言学中，对于 meaning最常见的解释为：

signifier ⟺ signified (idea or thing) = denotation

在计算机中我们该如何得到可用的词意

以上的定义由具体到抽象，在 NLP 领域中，主要是针对第一条 word representation进行研究。

最初 NLP 领域使用的是分类系统来对词的意思进行表示，比如 WordNet。我们可以通过查询单词的上位词以及同义词集来得知这个词的意思。

比如上图，我们查询 panda 的上位词，可以得到 procyonid (浣熊科)、carnivore (肉食动物) 等词。查询 good 的同义词，可以得到 full、 honorable、 beneficial、ripe 等词。

这就是一种离散的表示 (Discrete Representation)，然而这种表示方式存在很多的问题：

1. 词语有着独特的语境。以上面的同义词为例，在查询 good 的时候我们发现， ripe 和 honorable 都为其同义词，但是我们在描述一件事物为 good 的时候，如果使用其同义词 ripe 或者 honorable 来代替的话，很多时候都会显得很别扭。
2. 语言的变化日新月异，每天都有大量的新词涌现出来，而使用这种表示方式的话，很难及时更新旧词的含义和对新词进行定义。维护一个类似 WordNet 这样的数据库是需要花费大量的人力的，代价非常高昂。并且，使用人力去维护词库的话，必不可免地会存在人的主观性的影响。
3. 通过这种方式，我们能够得到的只是词的上下位词的信息，以及其同义词集信息，这种信息都只是一个二分类的结果，导致我们很难对于两个词之间的相似度给出一个准确的度量方式。

在绝大多数的基于规则和基于统计的 NLP 工作中，都将单词视为一种原子符号来进行处理。

比较常见的做法就是用 one-hot 向量来表示一个词，这是一种 localist representation。

从 symbolic representations 到 distributed representations

One-hot 看着是一种简单粗暴又可行的表示方法，然而在实际使用中，像 one-hot 这种离散的 symbolic representations 是存在一些问题的：

1. One-hot 向量是正交的，这种表示方法是无法得到不同单词间的相似度的。
2. One-hot 向量存在着数据稀疏的问题。
3. 因其表示的方式的问题，随着所用词表的扩增，One-hot 向量还会出现维度灾难。(Dimensionality: 20K (speech) – 50K (PTB) – 500K (big vocab) – 13M (Google 1T)

因而，我们需要去探讨一种新的词向量的编码方式。

You shall know a word by the company it keeps.

– J. R. Firth 1957: 11

这里就提出了一种思路，即我们可以通过一个单词的上下文信息中得到这个单词的意思。

这是现代统计自然语言处理最成功的思想之一，事实上这也是 Word2Vec 算法的根基。

Word2Vec

定义

首先我们需要先定义一下预测单词上下文的模型及损失函数：

$p(context | w_t) = …$

$J = 1 - p(w_{-t} | w_t)$

这里的 $w_{-t}$ 表示除了 t 之外的上下文。

Word2Vec 的主要思想

Word2Vec 有两种计算模型，两种模型的思路是截然相反的：

1. Skip-grams (SG) : 通过中心词来预测其上下文信息
2. Continuous Bag of Words (CBOW) : 通过上下文信息来预测中心词

先上一张课件中 SG 模型的预测图方便大家理解，这里我们就是通过 banking 这个中心词来对其上下文信息进行预测，学习的目的就是要最大化上下文中各词的条件概率。

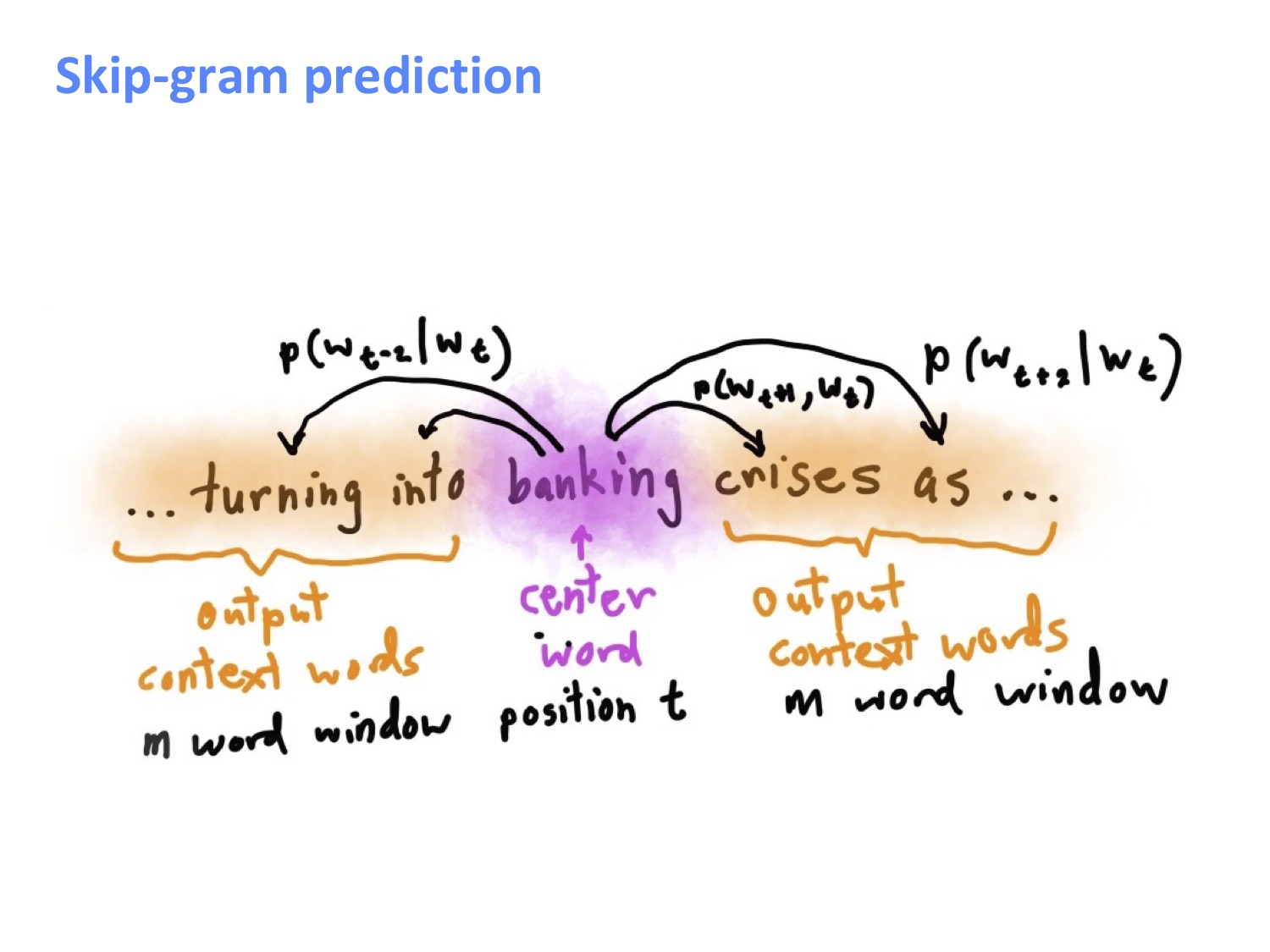
这里的上下文的条件概率 $p(w_{-t}|w_t)$ 是由 softmax 得到的：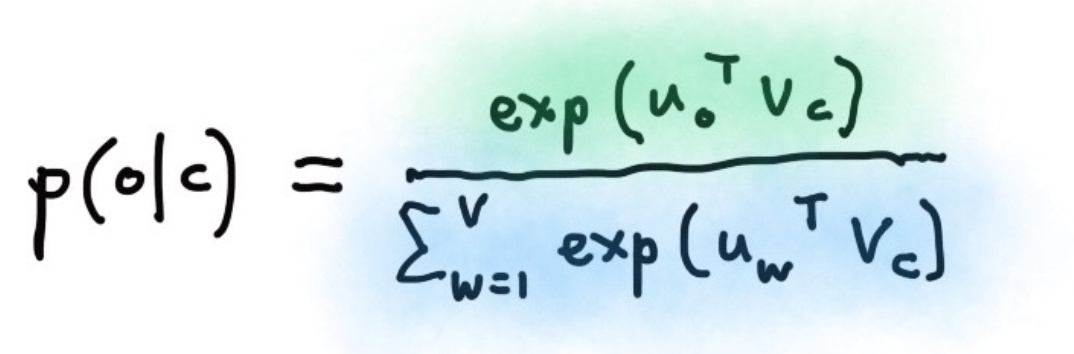

然后，目标函数定义为所有位置的预测结果的乘积：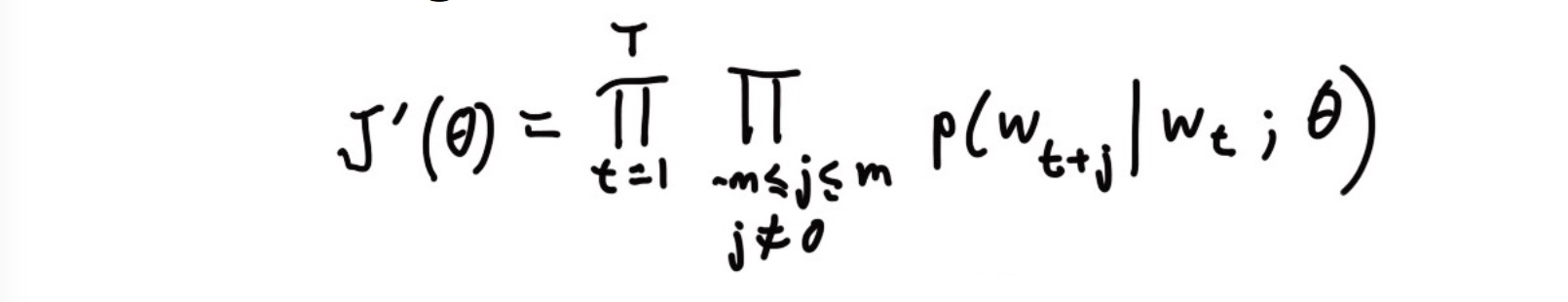

为了方便计算，加个负对数得到最终的损失函数，这样问题就转化为最小化损失函数了：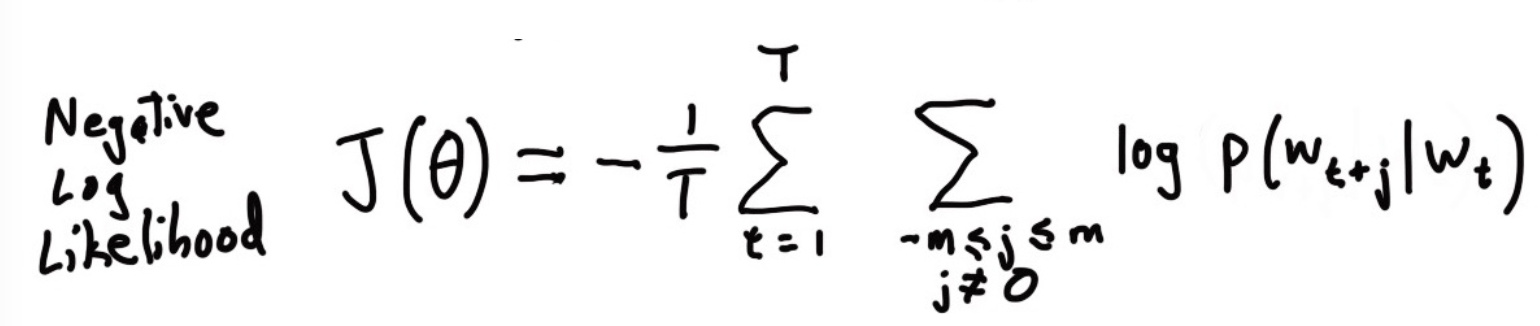

接下来就是上几张大家不知道见过多少遍的经典模型图了，以下分别为 CBOW 模型和 SG 模型：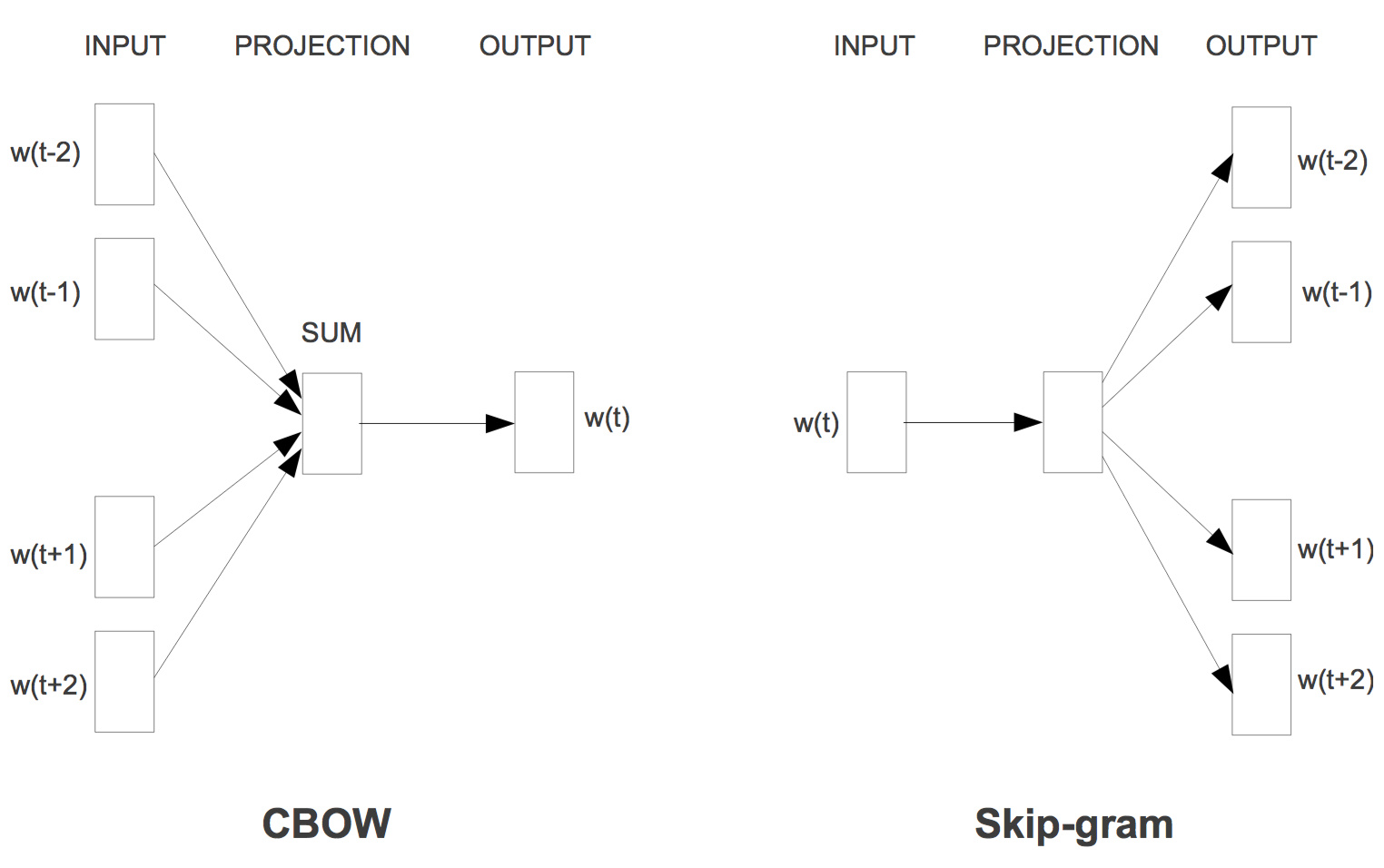

模型流程

这里参考知乎上crystlajj的回答，并偷懒盗用了不少图，以 CBOW 模型的流程为例：

1. 输入层：上下文单词的 onehot. {假设单词向量空间dim为V，上下文单词个数为C}
2. 输出层的 label ：中心词的 onehot。
3. 权重矩阵 W 和 W’：维度分别为 {V*N} 和 {N*V}，并将权重矩阵初始化。要注意最后得到的输入端的 W 即为单词的词向量表示，词向量的维度为N（每一列表示一个词的词向量）。
4. 所有上下文单词的 onehot 分别乘以共享的输入权重矩阵 W。
5. 将每个单词的 onthot 与 W 相乘所得的 {1*N} 维向量相加求平均作为隐层向量。并将得到乘以输出权重矩阵W’，得到一个 {1*V} 维的向量。
6. 将得到的 {1*V} 维向量经过 softmax 函数处理得到 V-dim 概率分布，概率最大的index所指示的单词为预测出的中心词（target word）。
7. 与true label的onehot做比较，损失函数越小越好。

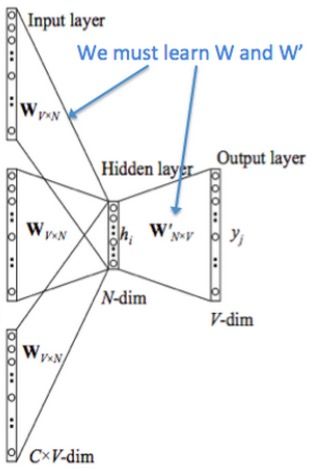
再偷几张图举个例子，让大家跟着走一遍CBOW模型的流程：

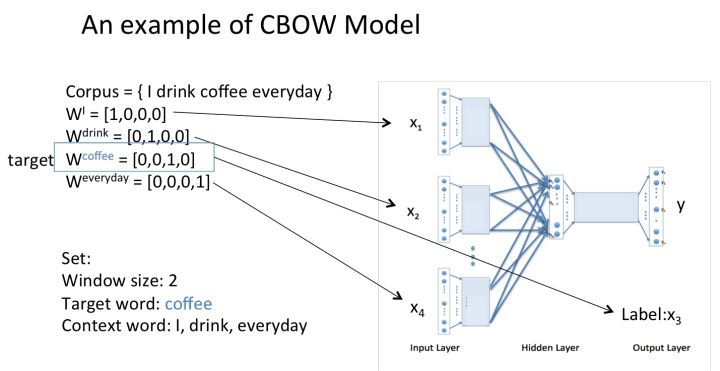
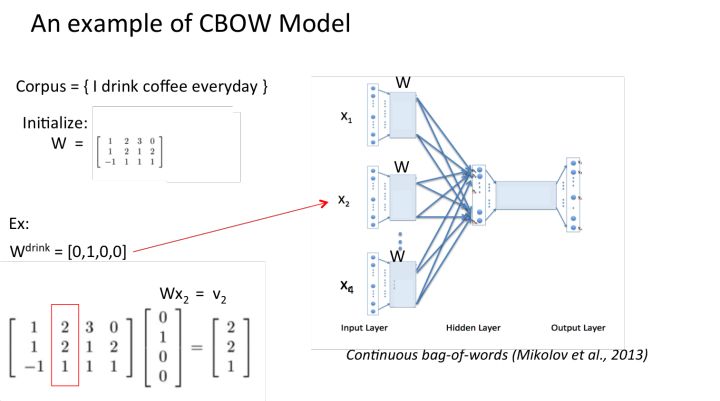
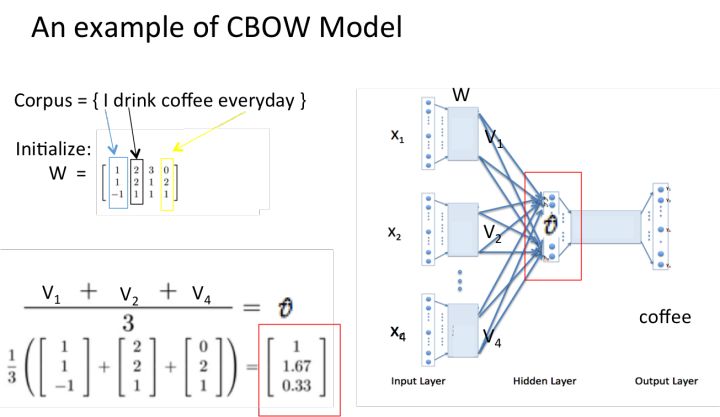
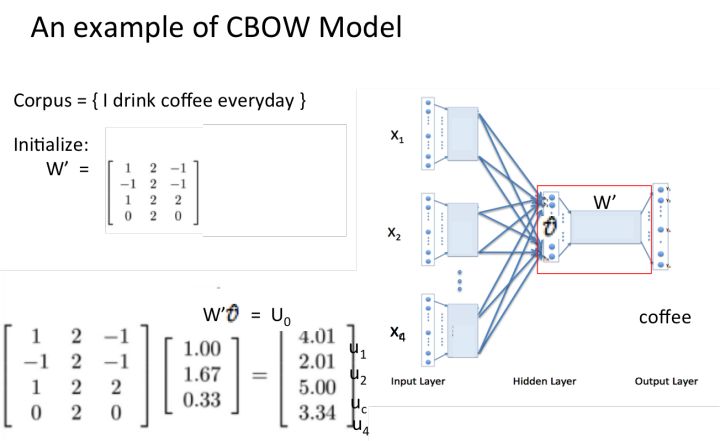
以上就是CBOW 模型的流程，这里再附上一张课件中给出的 SG 模型的流程，可以对比一下。

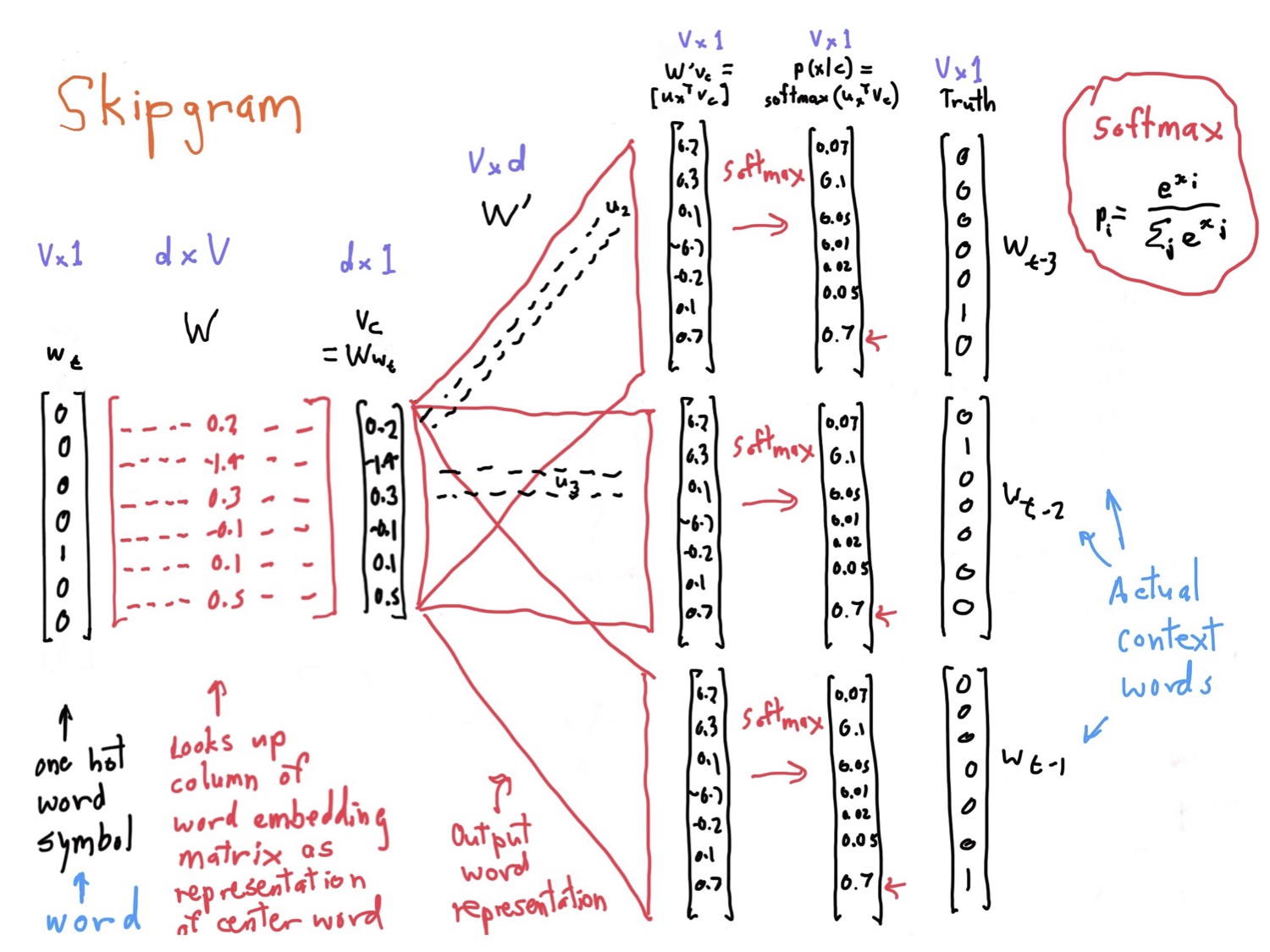
以上就是 Word2Vec 的两种模型的算法流程。其实这种 distributed representation 的思想其实很早就有了，而真正火起来是在 13 年 Mikolov 大神的两篇文章之后。

因为这个方法实际上存在着一些问题。比如训练词向量模型时我们输入端和输出端用到的依旧是 onehot 编码，维度灾难问题仍然存在。如果语料足够大的话，onehot 编码的长度就很大，每轮学习需要更新大量的参数，将会导致训练速度慢到难以接受的地步，如果语料不够充足的话，则很难学到高质量的词向量表达。

Word2Vec 优化

因而 Mikolov 大神就提出了两种高效的训练方法：

1. Hierarchical softmax
2. Negative sampling

这部分是课程里头没有涉及的内容，并且公式太多太繁杂，在这里只做一个大概的介绍（实在是懒得写了 doge），具体的推导和源码解析可以参考 falao_beiliu 和 Hankcs 的文章。

Hierarchical softmax

以 CBOW 为例，HS 的方法就是在输出层使用一颗 huffman 树来提升训练效率，模型图如下所示：

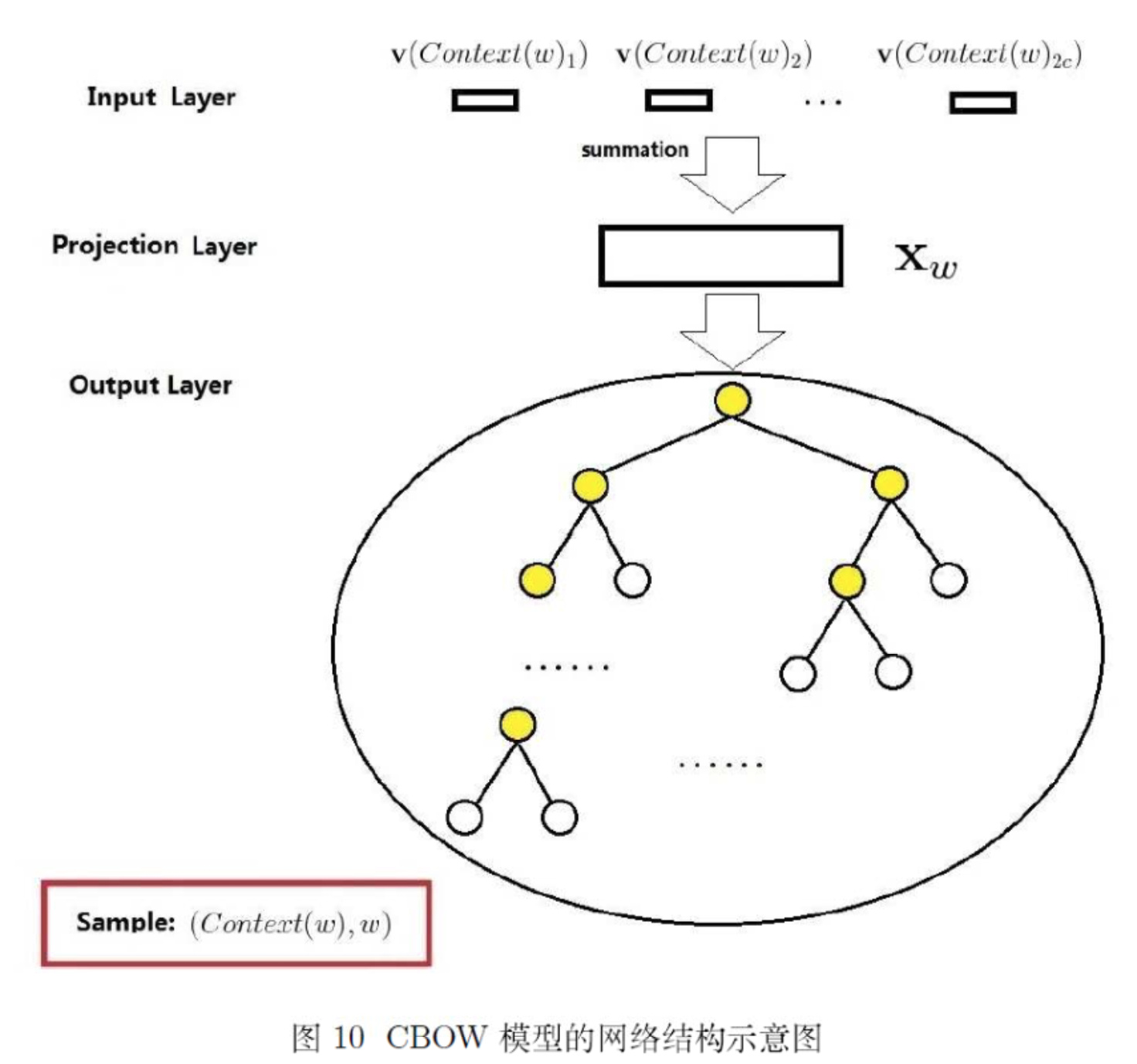
Huffman 树在这里就不科普了，HS 方法中的 huffman 树的每个叶子结点表示一个单词，可以被 01 唯一地编码。每个非叶子结点相当于一个神经元。

由于 huffman 树的特点可以使得编码长度最短，这里我们将单词以词频来建立huffman 树，就可以使得常用词的路径较短，非常用词的路径较长。HS 方法就可以将原本查找目标词的多分类问题转化为多个二分类问题，在每一个非叶子结点进行 softmax 运算，根据结果选择向左下走或者向右下走，进而直到走到叶子结点，就可以得知预测的目标词是什么。通过这种方法，我们每次更新的只是走过的路径上的参数，而非全部的参数，可以使得效率大幅度提高。

SG 模型的 CBOW 方法同理，结构示意图如下所示：

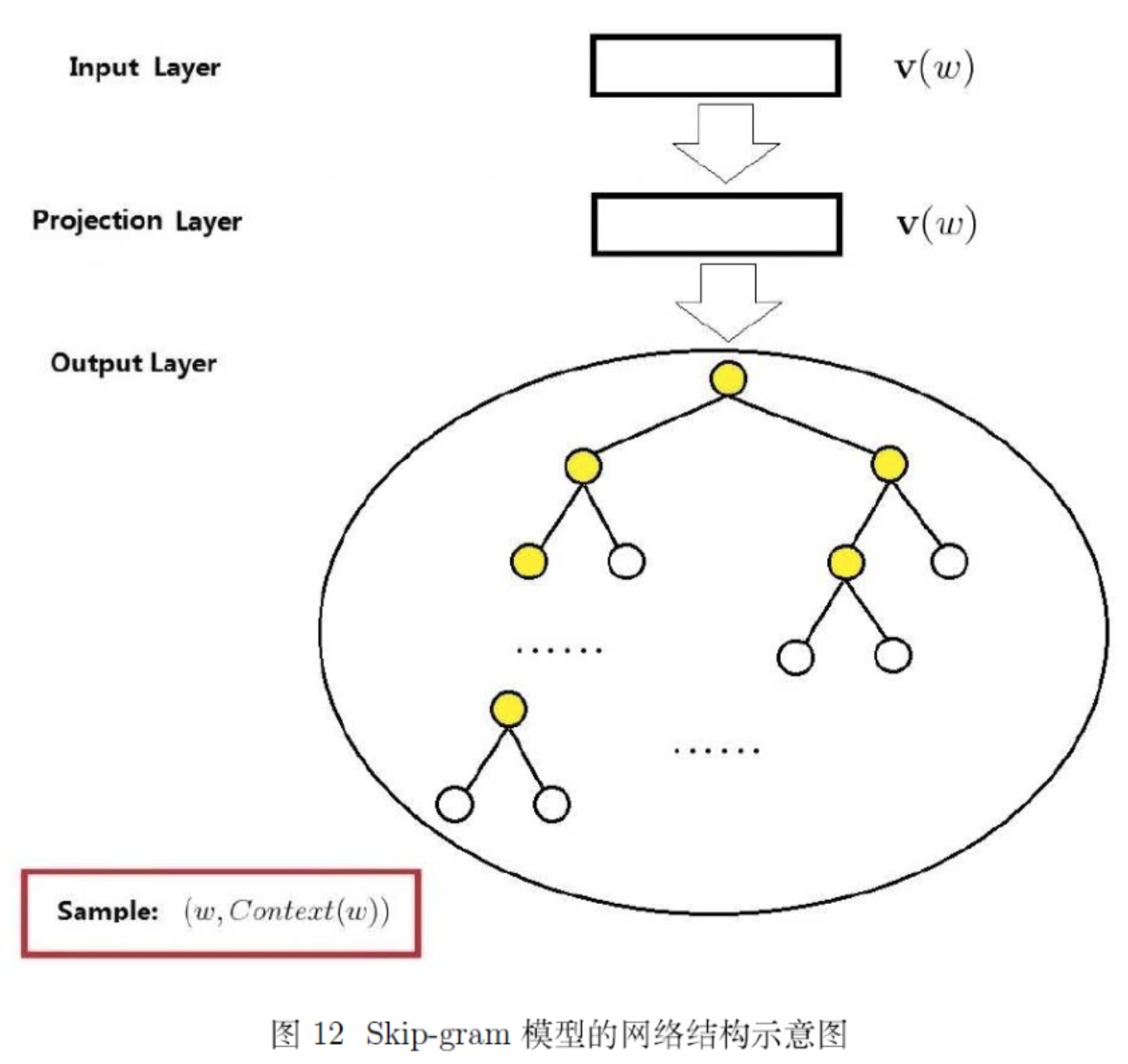
Negative Sampling

回想一下之前的算法，我们输出的 label 都是一个词的 one-hot 编码，维度为整个词库的大小，这里的目标词的 index 即为分类任务的正例，其他的词都为负例，也就是说在一个单词数为 N 的词库中，我们的分类任务的正例为 1，负例为 N - 1。正常 N 值会远远大于 1，但是每次更新中，所有的负例的参数权重也会跟着一块更新，在 Mikolov 看来这其实是一个很没有效率的事情，我们大可以把负例减少来提高效率并且对于最后的结果不会产生大的影响。

因此就提出了 NS 方法，顾名思义，NS 即随机挑选出一些负例。采样的算法思想都应该保证频次越高的样本越容易被采集到，因此，NS 算法基本的思路是对于长度为1的线段，根据词语的词频将其公平地分配给每个词语：

$len(w) = \frac{cnt(w)^N}{\sum_{u\epsilon D}cnt(u)^N}$

所以就可以根据词频来分配线段中每个词所占有的长度了。这里 Word2Vec 为了提高效率，用了点小 trick，即将原本线段标上 M 个刻度，这样就不需要浮点数的操作，而是直接使用 0-M 间的整数，经过查表就可以得知该取哪个单词了。

注意这个 len(w) 的计算有包含一个幂计算 (N)，这实际上是一种平滑的策略，可以增大低频词的值，使之更容易被采样到。

---

以上大概就是本节课的内容和扩展，实际上课程里头还包含了一些数学知识的复习和 sgd 算法的推导，觉得过于老生常谈，就不拿出来说了，之后如果有相似的内容也会一样跳过。

参考文献

1. cs224n lecture2
2. cs224n lecture2 slides
3. cs224n笔记2 词的向量表示
4. word2vec原理推导与代码分析
5. 深度学习word2vec笔记之算法篇