这节课一开始先回顾了一下上节课的内容,Word2Vec。
Word2Vec 总结
接着对 Word2Vec 算法作了一个总结:
- Word2Vec 遍历了整个语料库中的每一个词。
- Word2Vec 算法的主要思想为通过一个单词的上下文信息中得到这个单词的意思,即通过中心词来预测其上下文信息 (SG) 和通过上下文信息来预测中心词 (CBOW)。
- Word2Vec 捕获的是共现词中是否同时出现的信息。
这里由第 3 点引出了一种新的思路,Word2Vec 算法只是捕捉了两个词是否同时出现的信息,那我们是不是可以直接去捕捉单词间共现次数的信息呢?很显然答案是肯定的,这也就是本节课的内容,GloVe。
基于共现矩阵的词嵌入模型
在讲述 GloVe 算法之前,我们先讲一下较为原始的方法。首先我们需要通过大量的语料文本来构建一个共现矩阵 (Co-occurrence Matrix)。矩阵的构建方式有两种:document-based 和 windows based。
前者一般用于主题模型 (LSA),由于统计的是全文的信息,所以这种矩阵很难描述单词的语法信息。后者类似于 Word2Vec,需要指定一个统计的窗口大小,只在窗口的范围内统计单词的共现次数,这种方法可以同时捕捉到语法信息 (POS) 和语义信息。
举个例子,假设语料由三句话组成:
- I like deep learning.
- I like NLP.
- I enjoy flying.
那么如果我们把其窗口的大小设为1,并使用对称窗口的方法,则其共现矩阵如下:
| counts | I | like | enjoy | deep | learning | NLP | flying | . |
|---|---|---|---|---|---|---|---|---|
| I | 0 | 2 | 1 | 0 | 0 | 0 | 0 | 0 |
| like | 2 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| enjoy | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| deep | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| learning | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| NLP | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| flying | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| . | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
如果直接简单的以共现向量当做单词的词向量的话,虽然不同的词向量之间就不再像 One-hot 一样是正交的了,可以一定程度上用来计算单词间的相似度,但是还是存在许多问题:
- 随着词表的增加,词向量的维度也得跟着增加。
- 维度灾难问题。语料足够大的时候词表也会很长,导致向量长度过大,训练的代价高昂。
- 数据稀疏。与 One-hot 类似,共现矩阵中不为 0 的维度数量很少,会使得后续的分类模型鲁棒性下降。
共现矩阵的降维处理
为了解决以上问题,语言学家们自然而然地想到了将共现矩阵进行降维,进而得到单词的稠密表示 (dense representation)。
那么如何对共现矩阵进行降维呢?一个很常见的方法就是使用奇异值分解 (SVD)。SVD 的基本思想是,通过将原共现矩阵 X 分解为一个正交矩阵 U,一个对角矩阵 S,和另一个正交矩阵 V 乘积的形式,并提取 U 的 k 个主成分(按 S 里对角元的大小排序)构造低维词向量。具体原理推导可以参考 leftnoteasy的博文。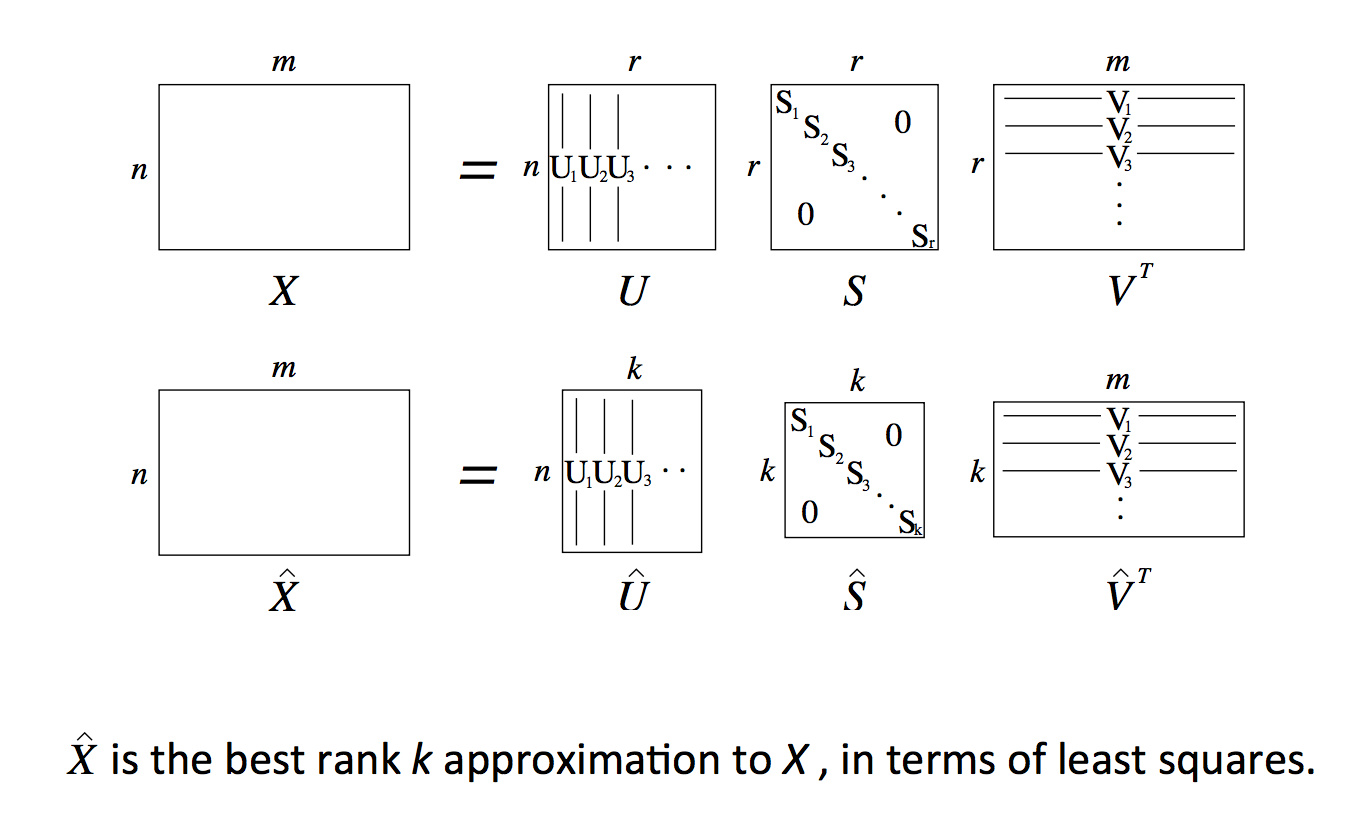
除此之外,对于共现矩阵 X 的处理也有很多值得一提的 Hacks:
- 部分的单词 (the, he, has) 出现的次数过多,使得它们对于语法信息的影响过大。改进的方法就是限制高频词的最大频次 (min(X, t), with t~100),或者干脆直接停用高频词。
- 带权重地统计窗口。距离中心词跃进的词对于词义的贡献就越大。
- 使用 Pearson 相关系数来替代掉词频,并把负值置 0。
以上的方法虽然简单粗暴,但是还是取得了很不错的结果。
然而 SVD 算法有几个根本性的问题没法解决:
- SVD 是一个计算复杂度高昂 (O($mn^2$)) 的算法,无法在实际环境中使用。
- SVD 方法不方便处理新词或者新的文档,如果加入一些新的语料后,就需要重新再进行 SVD。
- SVD 的画风跟其他的 DL 模型截然不同。
基于共现次数统计的方法 VS 直接进行预测的方法
讲完了 SVD 这类基于共现次数统计的方法和之前的 Word2Vec 这类直接进行预测的方法,课程中列出了以下这一张两种方法的对比图,两种方法的优势和劣势总结得十分到位。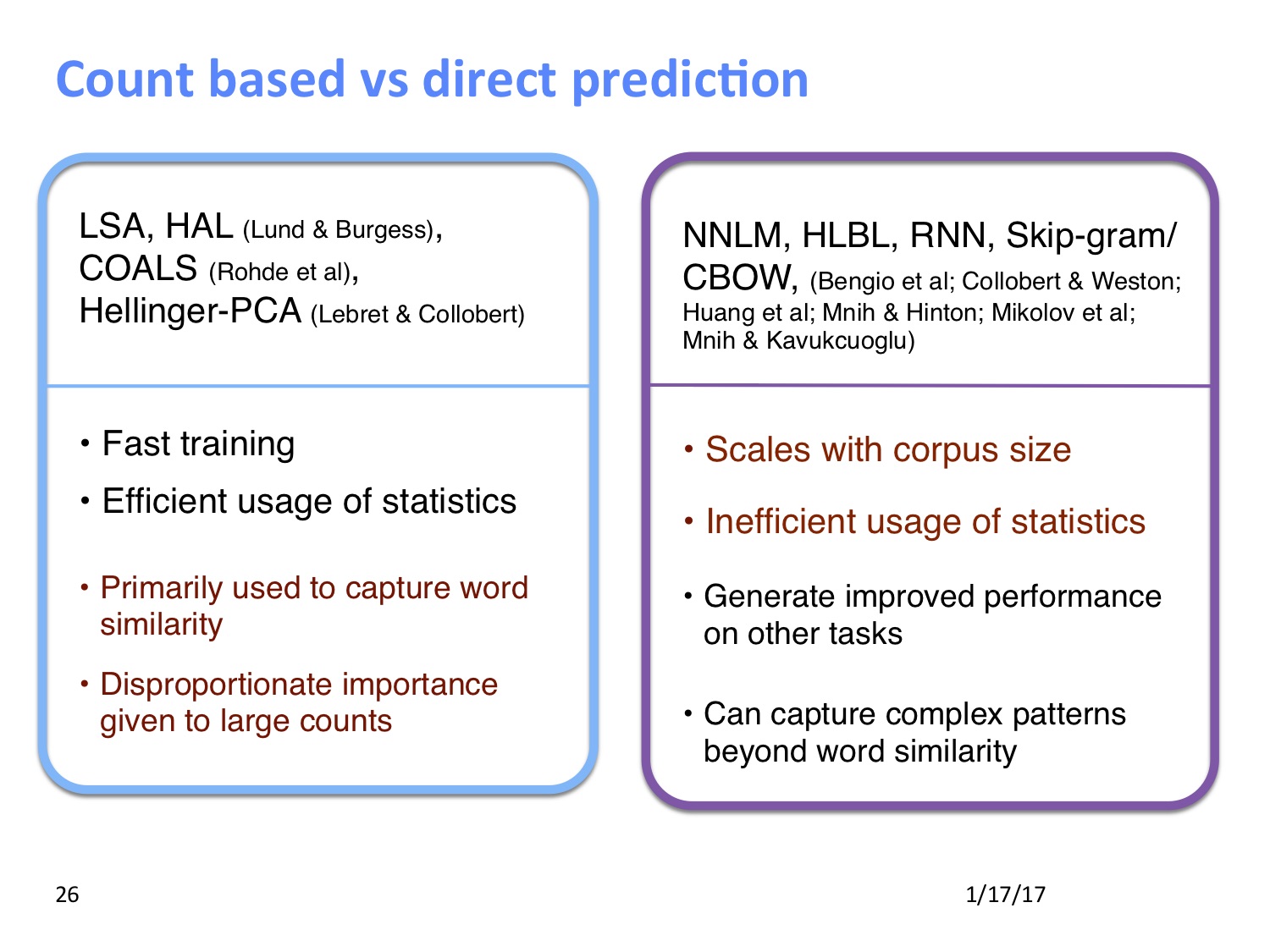
那么有没有一种方法能够同时结合以上这两种方法的优势呢?这就轮到本课的主题 GloVe 出马了。
GloVe (Global Vectors)
为了结合以上两种方法的优势,GloVe 模型既使用了语料库的全局统计特征 (全局共现次数统计),也使用了局部的上下文特征 (窗口)。因而 GloVe 模型引入了共现概率矩阵 (Co-occurrence Probabilities Matrix)。
直接上论文中的例子:
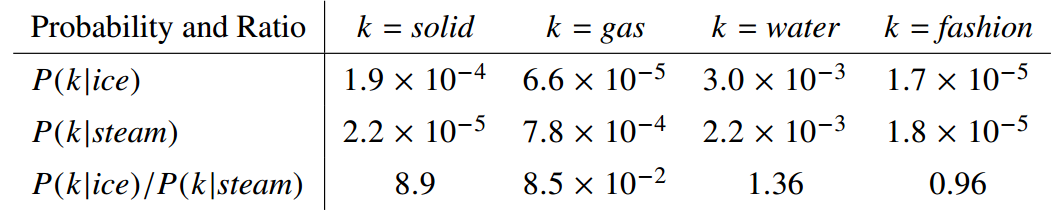
该矩阵的第一个元素为 ice 出现时 solid 出现的概率,第二个元素为 ice 出现时 gas 出现的概率,以此类推。由共现概率矩阵的值可以看出,概率比率 ($F(w_i, w_j, \hat w_k) = \frac{p_{i,k}}{p_{j,k}}$) 的取值是有一定规律的。
规律总结如下:
| $F(w_i, w_j, \hat w_k)$ | $w_j, w_k$ 相关 | $w_j, w_k$ 不相关 |
|---|---|---|
| $w_i, w_k$ 相关 | 趋近 1 | 很大 |
| $w_i, w_k$ 不相关 | 很小 | 趋近 1 |
也就是说,与原本的概率值相比,概率比例能够更好地表示出两个单词间的相关关系。这是一个很简单但是很有用的规律,如果我们用词向量 $w_i, w_j, w_k$ 通过某种函数计算 $F(w_i, w_j, \hat w_k)$,能够同样得到这样的规律的话,就意味着我们词向量与共现矩阵具有很好的一致性,也就说明我们的词向量中蕴含了共现矩阵中所蕴含的信息。
于是接下来就到了原作者神奇的脑洞时间了。
先上公式:$F(w_i, w_j, \hat w_k) = \frac{p_{i,k}}{p_{j,k}}$
这里等号的左端为全局统计求得的值,右端的 $w_i, w_j, w_k$ 就是我们要求得的词向量,而函数 F 是未知的,作者确定 F 的过程真是让人瞠目结舌。过程如下所示:
- $\frac{p_{i,k}}{p_{j,k}}$ 这个值考察了 $w_i, w_j, w_k$ 三个词两两之间的相关关系,但是这样很难进行 F 的求解,所以更好的方法是先去考察 $w_i, w_j$ 两个词之间的关系,线性空间中的相似性关系自然想到的是两个向量的差 $(w_i - w_j)$,所以我们可以把 F 的形式转化为 $F(w_i - w_j, w_k) = \frac{p_{i,k}}{p_{j,k}}$。
- $\frac{p_{ik}}{p_{jk}}$ 是一个标量,而 F 是直接作用在 $w_i - w_j$ 和 $w_k$ 这两个向量上的,为了把向量转化为标量,自然地就想到了用内积的方法,所以我们可以把 F 的形式进一步转化为 $F((w_i - w_j)^T w_k) = F(w_i^Tw_k - w_j^Tw_k) = \frac{p_{i,k}}{p_{j,k}}$。
- 此时 F 的公式的形式为 $F(w_i^Tw_k - w_j^Tw_k) = \frac{p_{i,k}}{p_{j,k}}$。等号左边为差的形式,右边则是商的形式,要把差和商关联起来,作者又想到了用取指数的形式,即 $\exp(w_i^Tw_k - w_j^Tw_k) = \frac{\exp(w_i^Tw_k)}{\exp(w_j^Tw_k)} = \frac{p_{i,k}}{p_{j,k}}$。
- 现在形式就很明朗了,我们只需让 $\exp(w_i^Tw_k) = p_{i,k}, \exp(w_j^Tw_k) = p_{j,k}$ 等式就能够成立。
- 那么如何让 $\exp(w_i^Tw_k) = p_{i,k} = \frac{x_{i,k}}{x_i}$ 成立呢?只需让 $w_i^Tw_k = \log\frac{x_{i,k}}{x_i} = \log x_{i,k} - \log x_i$。
- 又因为作为向量,i 和 k 的顺序交换后 $w_i^Tw_k$ 和 $w_k^Tw_i$ 应该是相等的,即它们应该是对称的。但上式的右边显然不符合这个条件,所以为了解决这个问题,作者又引入了两个偏置项 $b_i, b_k$,这样模型就变成了 $\log x_{i,k} = w_i^Tw_k + b_i + b_k$,其中 $b_i$ 包含了 $\log x_i$。此外还加入了 $b_k$ 来保证模型的对称性。
- 因此,我们就可以得到 GloVe 的目标函数了:$J = \sum_{i,k}(w_i^Tw_k + b_i + b_k - \log x_{i,k})^2$。
- 再考虑到出现频率越高的词对权重的影响应该越大这个原则,我们需要在目标函数里加一个频率权重项 $f(x_{i, k})$,所以最终的目标函数为:$J = \sum_{ik}f(x_{i,k})(w_i^Tw_k + b_i + b_k - \log x_{i,k})^2$。
对于这个频率权重项 $f(x_{i, k})$ 我们需要确保其为非减的,并且类似于之前对 (the, he, has) 这类常见词的处理方式,当词频过高的时候,频率的权重项不应该过大,因而需要将 $f$ 控制在一个合适的范围,所以频率权重函数 $f$ 的公式如下:
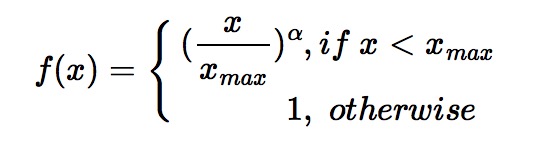
最终作者经过实验得出当 $x_\max = 100, \alpha = 0.75$ 是一个比较好的选择。
以上就是 GloVe 算法的完整推导流程,这里可以看到,最终我们得到的是 $w_i, w_k$ 两个权重矩阵,它们都捕捉到了单词的共现信息,在实际使用中,实验证明直接将二者简单的相加,得到的权重矩阵就是效果最好的词向量表示,即 $w_{final} = w_i + w_k$。
GloVe 优点
- 训练速度快。
- 可以扩展到大规模的语料。
- 也适用于小规模语料和小向量。

如何评估词向量
评估词向量质量高低的方法分为两种: Intrinsic (内部) 和 extrinsic (外部)。
Intrinsic
Intrinsic 评估的方式为专门设计单独的试验,由人工标注词语或句子相似度,与模型结果对比。
这种方法看似比较合理,并且计算速度也很快,然而却不一定对实际应用有帮助。有时候你花很多时间来调整词向量,使得内部评估方式的得分看起来很高,结果在实际应用上一跑预测结果却下降了。(尴尬又不失礼貌的微笑.jpg)
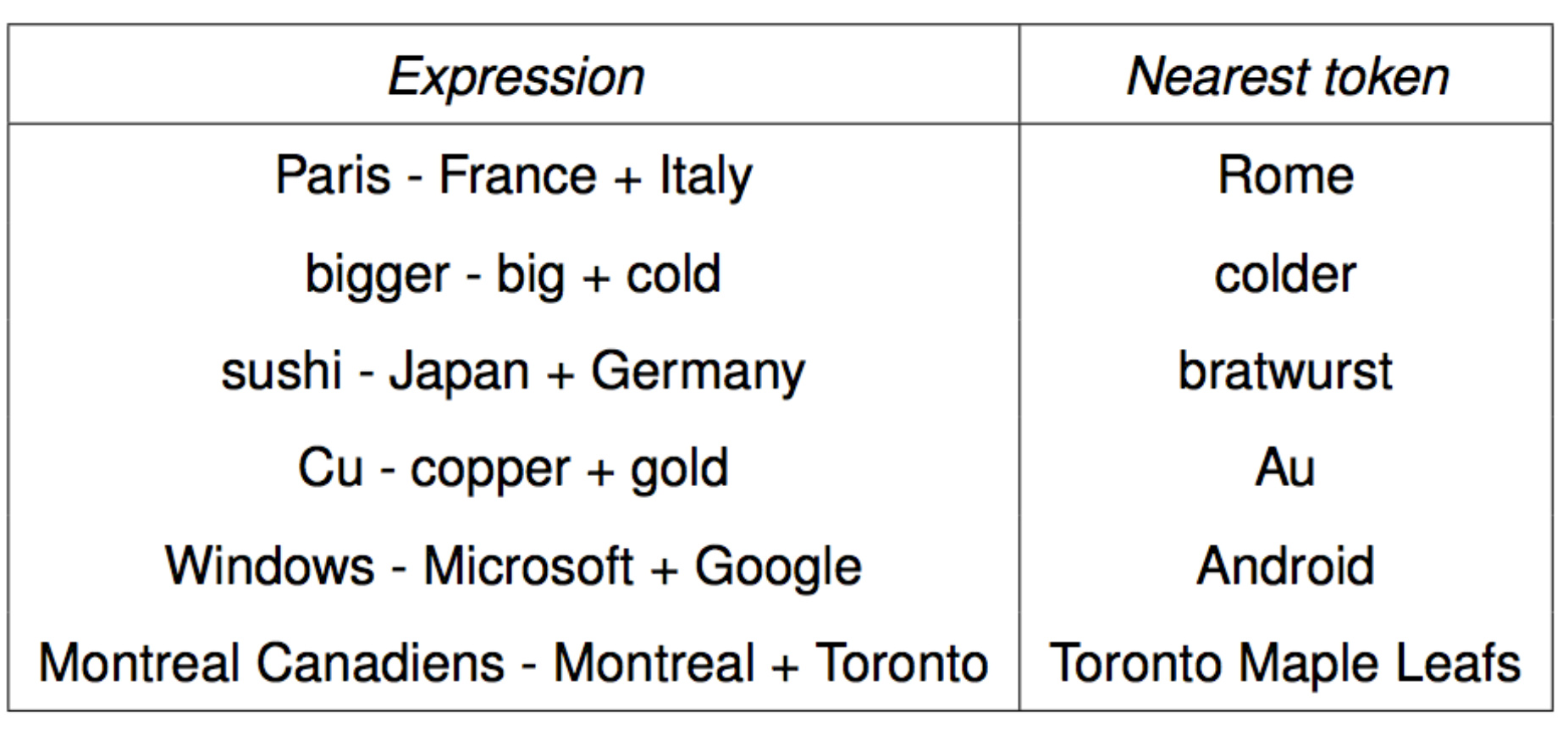
对于词向量模型来说,一个常用的 Intrinsic 评估是向量类比 (word vector analogies),它评估了一组词向量在语义和句法上表现出来的线性关系。

以上例而言,我们给定了一组词 $(a, b, c, d)$ 我们要验证的是 $d$ 与向量 $(x_b - x_a + x_c)$ 的余弦距离的值要最接近于 $d$ 这个词本身。
Extrinsic
Intrinsic 评估的方式为通过对外部实际应用的效果提升来体现。
耗时较长,不能排除是否是新的词向量与旧系统的某种契合度产生,需要至少两个subsystems同时证明。这类评测中,往往会用pre-train的向量在外部任务的语料上retrain。
词向量训练经验
直接上结论:
- GloVe 的效果在一些任务上可能会比 Word2Vec 更好,但有些时候二者并没什么区别,由于 Word2Vec 出现得更早,原理也更简单易懂,因而目前为止使用得还是很广泛的。
- 语料质量 > 语料数量。记得有某个 kaggle 的关于 Quora 句子相似度的比赛,我们组使用了个不错的模型,结果被其他组用普通的 LSTM 模型吊打得花枝乱颤,归其原因除了预处理没有做好外,我们使用的是泛用的语料训练得到的词向量,而那组人用的是专门的 Quora 语料。
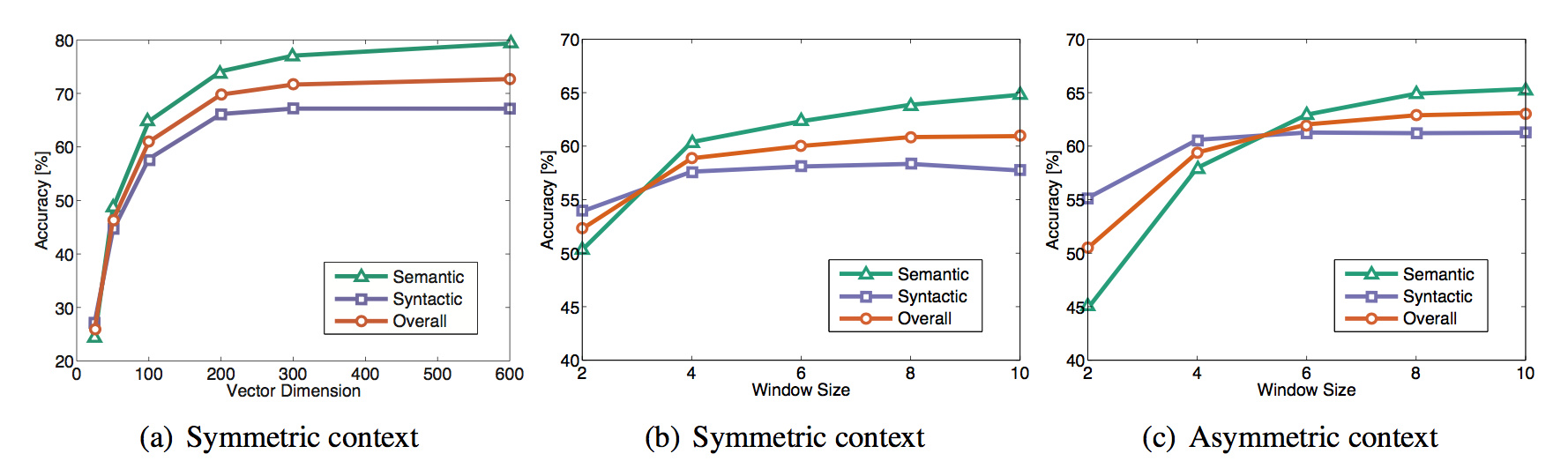
- 向量维度、窗口大小、窗口是否对称对词向量质量也有影响,具体如图。然而这是人类语言中的效果图,在不同的领域中参数还是需要根据实际情况来调整的。比如我之前做的 RNA 序列问题,最终最好的结果所取的窗口大小大于图中所示,向量维度反而是小于的。
- GloVe 相比 Word2Vec 更加稳定。
- 维基百科的语料好于新闻的语料。
- 在训练集大小较小的时候,在模型的训练过程对词向量进行 retrain 的话,会导致整个向量空间原有的几何结构被破坏,从而使得泛化能力变差,所以当训练集不够充分的时候不要 retrain 词向量。当训练集足够大的时候,retrain 词向量往往可以使预测精度得到提升。
- 从菜爸爸那里得知的一个 trick,可以同时使用两个 pretrain 的词向量,一组固定,一组随着模型的训练进行 retrain,可以使得精度提高。


