这节课 Socher 小哥讲的是根据文本的上下文来进行分类预测的问题。
分类任务
分类问题是很常见的机器学习任务了,在 NLP 领域,比较常见的分类例子有常见的情感、命名实体、决策等机器学习也常做的分类问题,也有通过上下文来预测其他单词的 (e.g. 阅读理解的填词),还有直接预测句子的 (e.g. 翻译)。
直观的分类
传统机器学习中经常使用的是 LR, SVM 之类的方法来找到分类的决策边界。
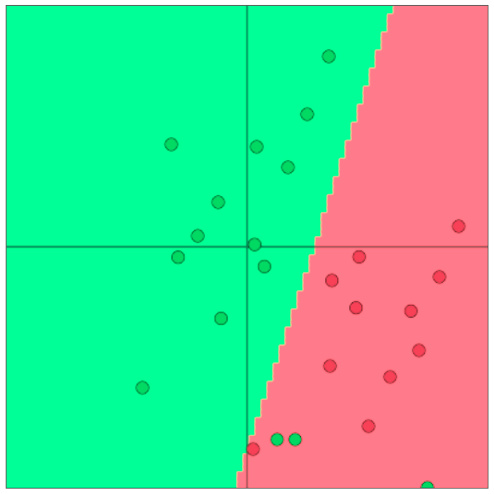
Softmax
这又是个大家常见的老朋友了,softmax 函数为 $p(y_j = 1|x) = \frac{\exp(W_jx)}{\sum_{c=1}^C \exp(W_cx)}$。
训练时候当然是为了让其概率 $p$ 最大了,所以为了方便计算,我们可以对概率取个负的对数作为其目标函数,其实这个损失函数就等同于交叉熵了。
$\begin{eqnarray} H(\hat y,y)&=& -\sum_{j=1}^{|V|}y_j\log(\hat y_j) \ &=& -\sum_{j=1}^{C}y_j\log(p(y_j=1|x)) \ &=&-\sum_{j=1}^Cy_j\log(\frac{\exp(W_jx)}{\sum_{c=1}^C \exp(W_cx)}) \end{eqnarray}$
即 $H(p, q) = -\sum_{c=1}^C p(c)\log q(c)$,交叉熵也可以被重新写成 KL 散度的形式:$H(p,q) = H(p) + D_{KL}(p||q)$。因为 $H(p)$ 在这里是为 0 的 (即使不为 0,那它也是一个固定值,对于优化并没有什么帮助),所以要最小化这个等式就等同于最小化 KL 散度。
这里要注意的一点是 KL 散度并非是指距离,而是一种非对称的衡量 $p$ 和 $q$ 之间概率分布差异的标准,其具体公式为 $D_{KL}(p||q) = \sum_{c=1}^C p(c)\log\frac{p(c)}{q(c)}$。
我们回到之前的 $H(p, q)$ ,因为这里的 $p$ 是 one-hot 的,所以实际上剩下的就只有正类的负对数项了,所以在整个数据集 ${x_i,y_i}^N_{i=1}$ 的目标函数为:$J(\theta) = \frac{1}{N}\sum_{i=1}^N-\log(\frac{e^{f_{y_i}}}{\sum_{c=1}^C e^{f_c)}})$。
再加上正则项即可得最终的目标函数为:$J(\theta) = \frac{1}{N}\sum_{i=1}^N-\log(\frac{e^{f_{y_i}}}{\sum_{c=1}^C e^{f_c)}}) + \lambda\sum_k \theta_k^2$。
分类任务中词向量的更新
在传统的机器学习问题里,模型的参数是由那些权值矩阵 $W$ 的列组成的,一般都不会太大,我们只需要更新它的决策边界:
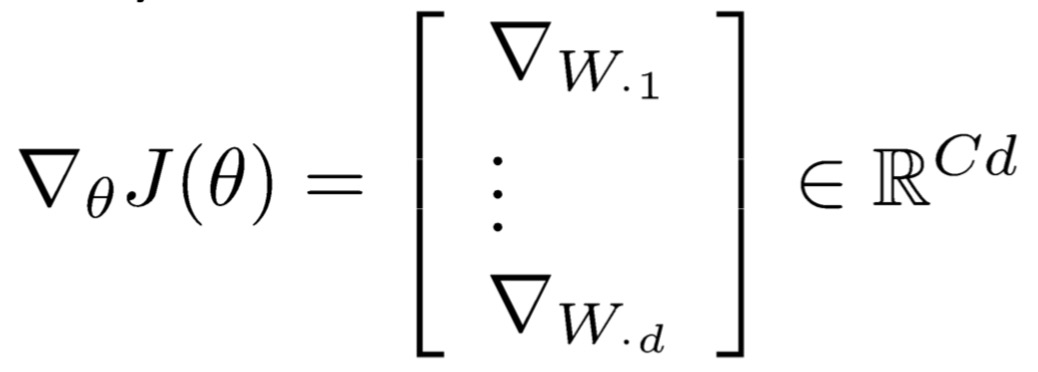
而在深度学习里,情况就截然不同了,我们除了更新决策边界之外,还可以更新我们的词向量 $x$:
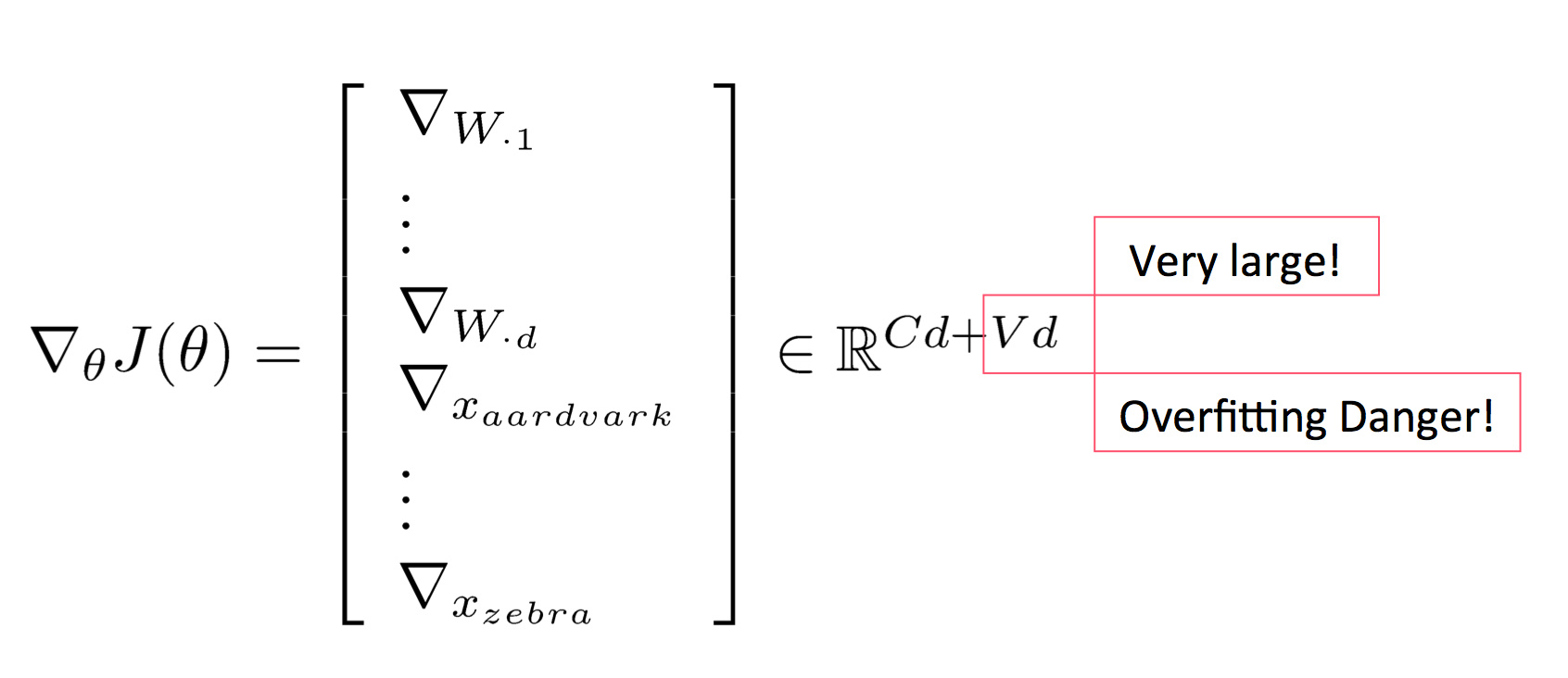
要知道参数一多,模型就容易发生过拟合,课程中举了一个例子。在预训练的词向量里,”TV”, “telly” 和 “television” 这三个词是一块的,但由于情感分类的语料中的训练集只包含 “TV” 和 “telly”,导致 re-training 后这两个词跑到其他地方去了,不再跟其同义词 “television” 一起。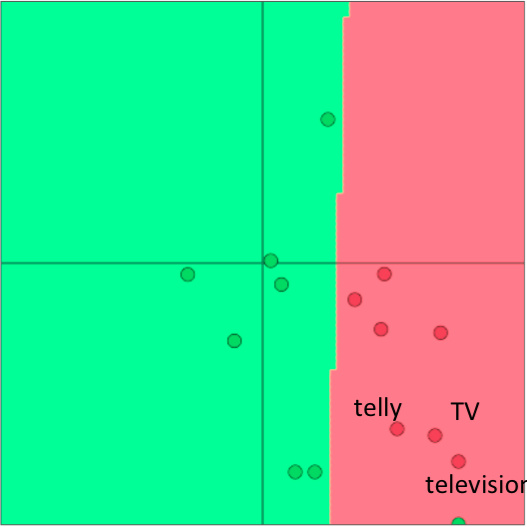
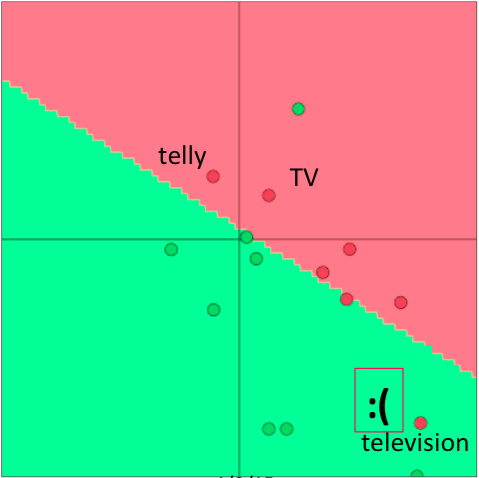
那么什么时候应该 re-train 词向量,什么时候又该使之固定不动呢?Socher 小哥给出了一点人生经验:如果训练集较小的时候,就不要再训练词向量,因为这样会破坏其原有结构;如果我们有一个很大的训练集的话,那我们在训练模型中也一并再训练词向量将会取得更好的效果。
窗口分类
在文本分类的任务中,我们其实是很难对于单个单词来进行分类的,因为语义中会有歧义出现,例如: “to sanction” 的意思可以是 “to permit” 或者 “to punish”;”to seed” 的意思可以是 “to place seeds” 或者 “to remove seeds”。
而在命名实体中也很容易产生歧义,例如:”Paris” 可以指 “Paris, France”,也可以指 “Paris Hilton”,”Hathaway” 可以指 “Berkshire Hathaway”,也可以指 “Anne Hathaway”。
那么该如何去消除这些歧义呢?一个很自然而然的想法就是用上这个单词的上下文信息。
有种做法是将窗口内的词向量来求一个均值 / 加权均值,但是这样会丢失其位置信息。
还有另外一种做法是将其窗口内的词向量给拼接起来,例如我们取窗口长度为 2,则新的向量的维度为 $X_{window} = x \epsilon \mathit{R}^{5d}$。
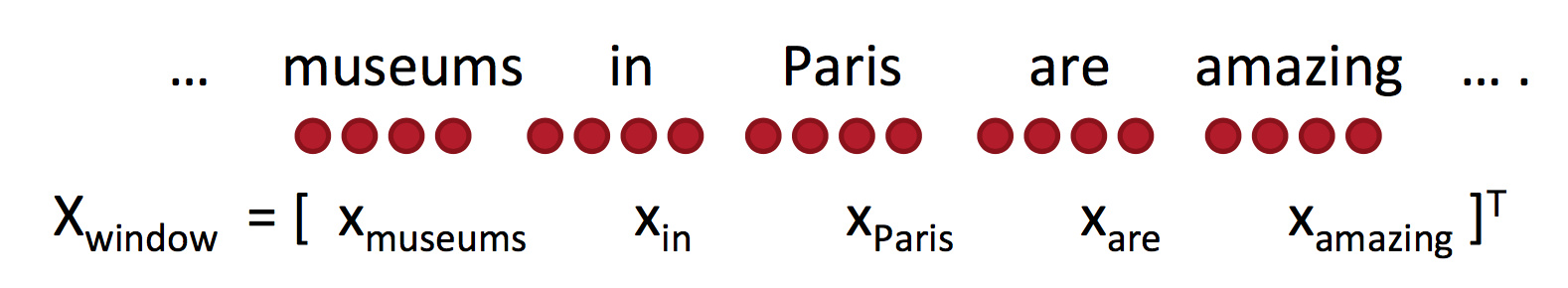
那么如何对这种拼接起来向量进行更新呢?答案是跟原本一样,我们可以将该词向量再拆分开来算,只是我们需要更加小心别算错了。这里需要知晓的是,在更新过程中,计算代价比较高的有两部分:矩阵乘法 $f = Wx$ 和 $\exp$。当然,矩阵乘法的速度还是比循环快很多。
这种拼接的方法是很有好处的,比如之前的 “Paris” 的例子,假如我们在其窗口内发现了 $X_{in}$ 这个词向量,就知道它代表的是一个地名而非人名了,这样歧义就消失了。
softmax (= LR) 的分类效果其实是十分有限的,它只是一种线性的分类器:
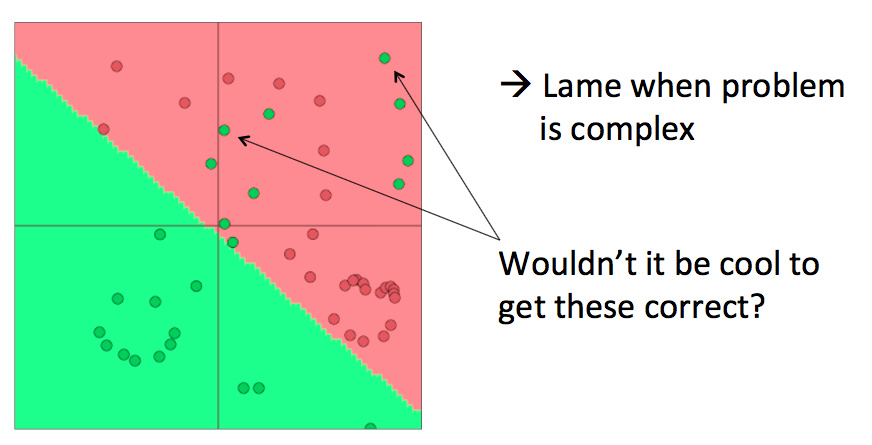
而神经网络则可以提供非线性的决策边界:
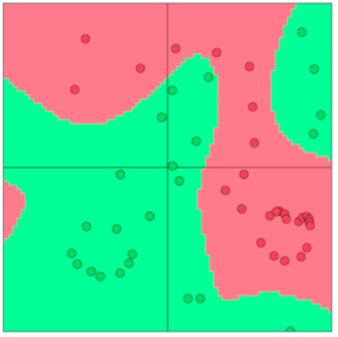
神经网络
这里课上又讲了一些神经网络的基本知识,包括神经元、激活函数、前向传播、反向传播、链式求导之类的老调调,这里就偷懒不写了 。
关于 BP 算法,这里有篇文章我觉得写得不错。
间隔最大化目标函数
最后选择性得写一下目标函数,在设计目标函数的过程中,我们用 $S$ 表示正确分类的得分,$S_c$ 表示误分类的得分。其中 $S = U^Tf(Wx+b), S_c = U^Tf(Wx_c + b)$,我们通过负采样来得到负例。
一种很朴素的想法是直接最大化 $(S - S_c)$,也就是说我们只需要要求 $S$ 的值高于 $S_c$ 就可以了,并不要求两个值的实际大小为多少,我们在计算损失的时候只需简单地计算 $(S_c - S) > 0$ 时候的错误。这种限制下的目标函数为:$J = \max(S_c - S, 0)$。
这么做的要求实在太低了,我们可以往这里加入一个缓冲区域,令 $J = max(1 - S + S_c, 0)$。
这种做法可以让我们在训练中更加关注那些难以区分的样本。


