印象中几乎所有 ML / DL 课程都会介绍一遍 BP 算法,本门课也绕不过 BP 这座山。这节课主要介绍的是 BP 算法和对课程项目的一些建议,因为前者已经是老生常谈的了,所以只能写写后者了。
本门课程是从 4 个不同的角度来讲解 BP 算法的:
通用公式
关于 BP 算法的通用公式推导,我还是继续安利一下这篇文章。
电路图
课程中举了这么一个例子,我们可以将函数 $f(x,y,z) = (x+y)z$ 视为下图的加法器和乘法器电路:
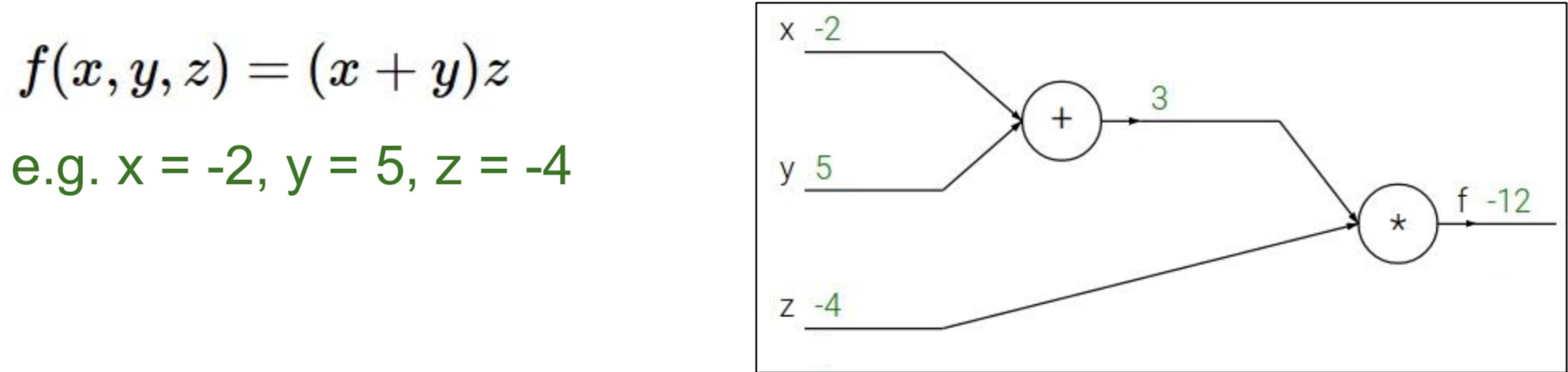
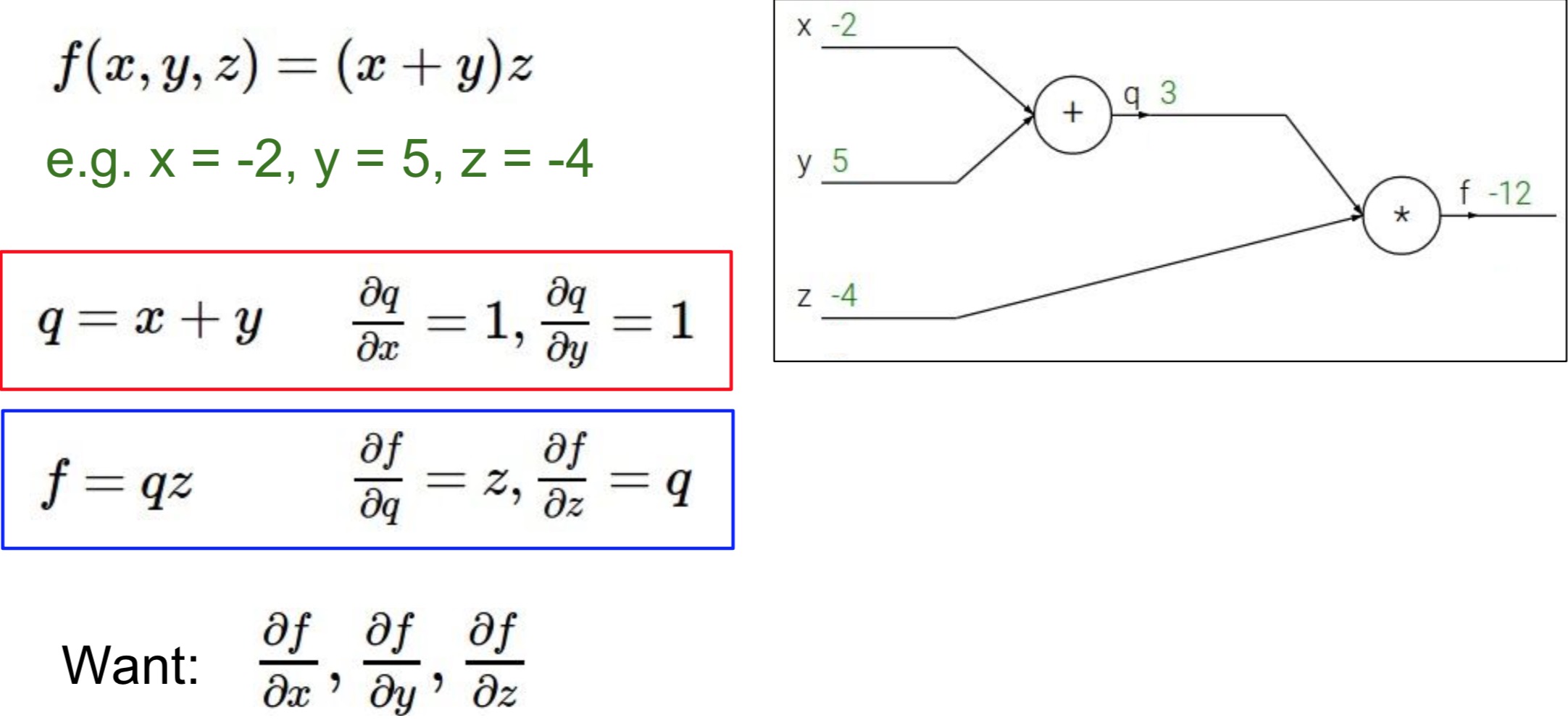
为了方便计算,我们把中间过程给表示出来,令 $q = x+y , f = qz$,所以则有 $\frac{\partial q}{\partial x} = 1,\frac{\partial q}{\partial y}=1,\frac{\partial f}{\partial q} = z,\frac{\partial f}{\partial z} = q$。从而问题变为求 $\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z}$,如下图所示:
接着我们从输出到输入一步步地分别反向求导计算,过程如下面图片所示:
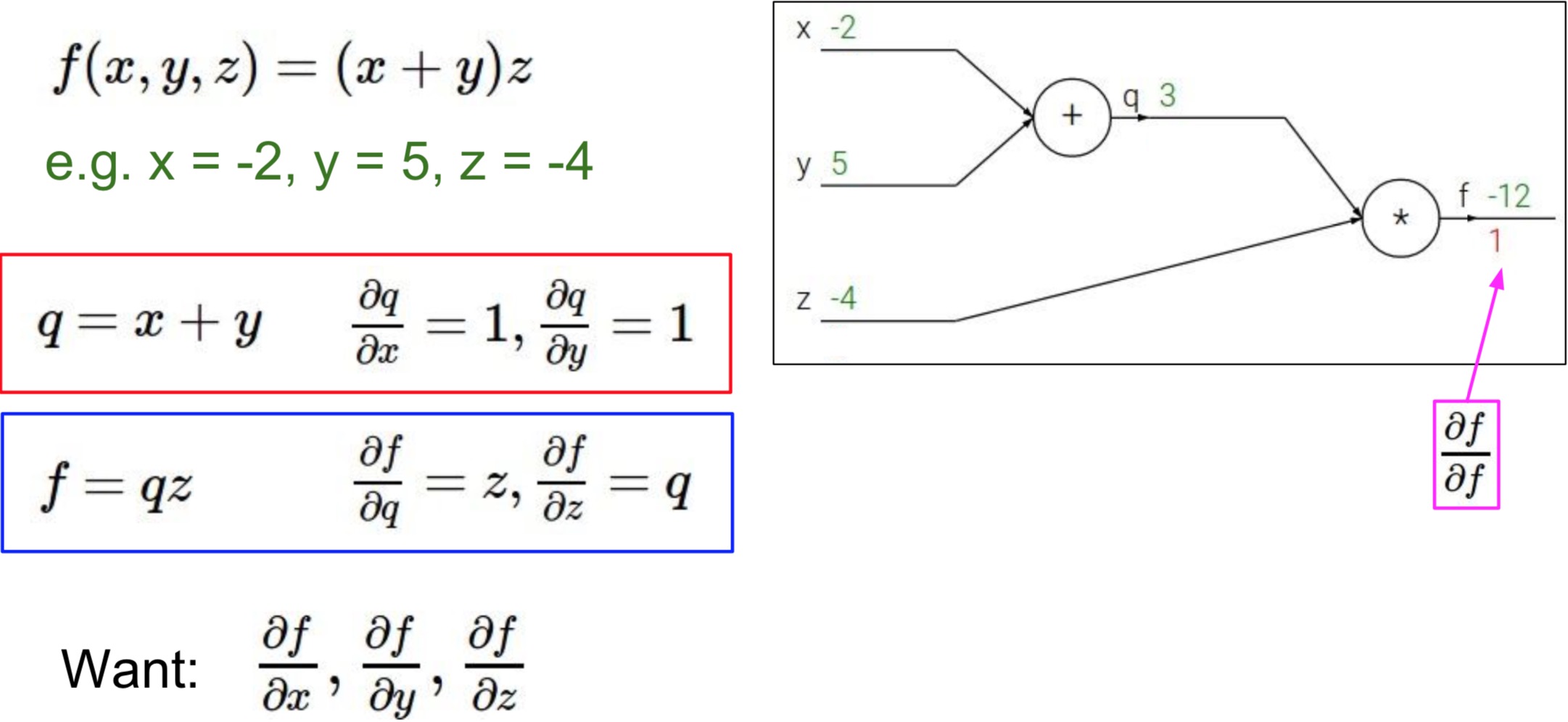
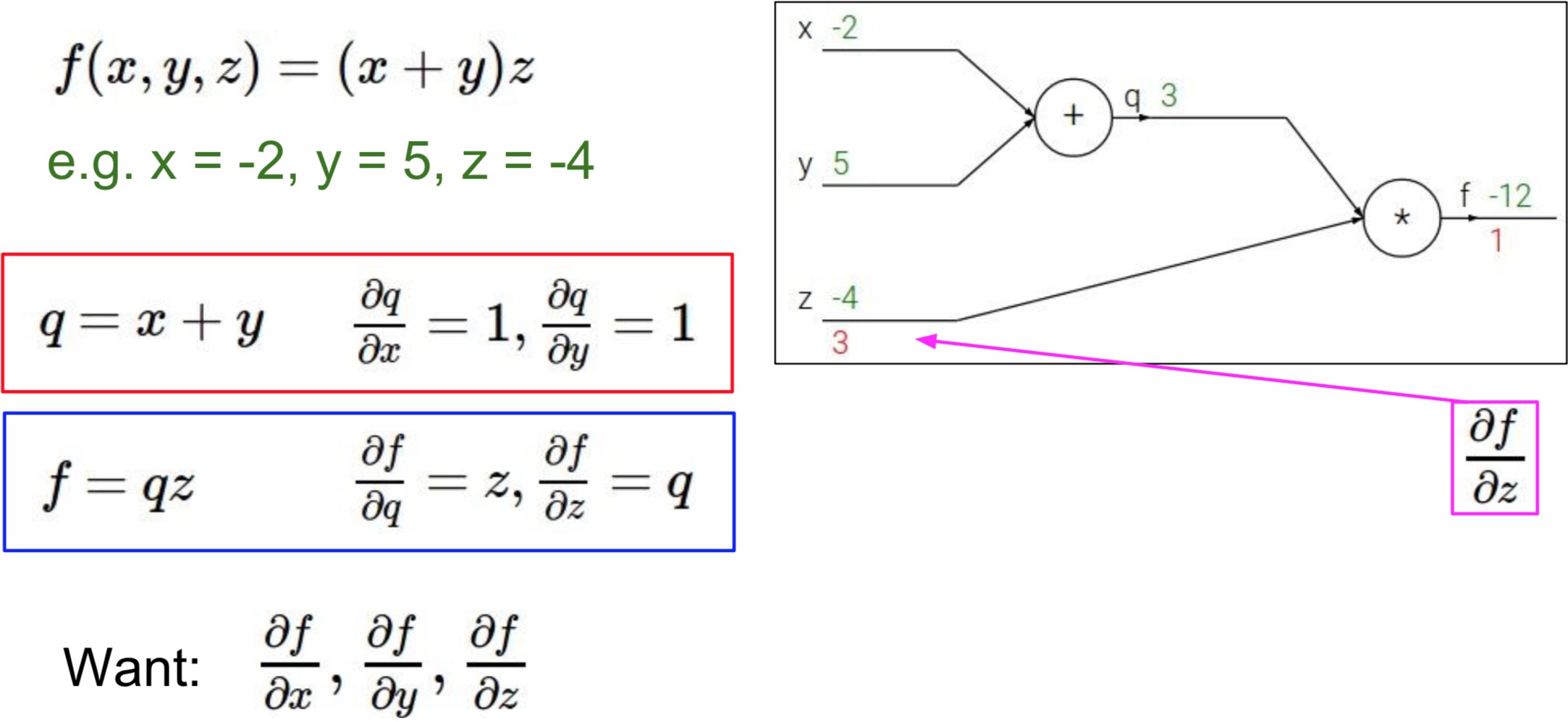
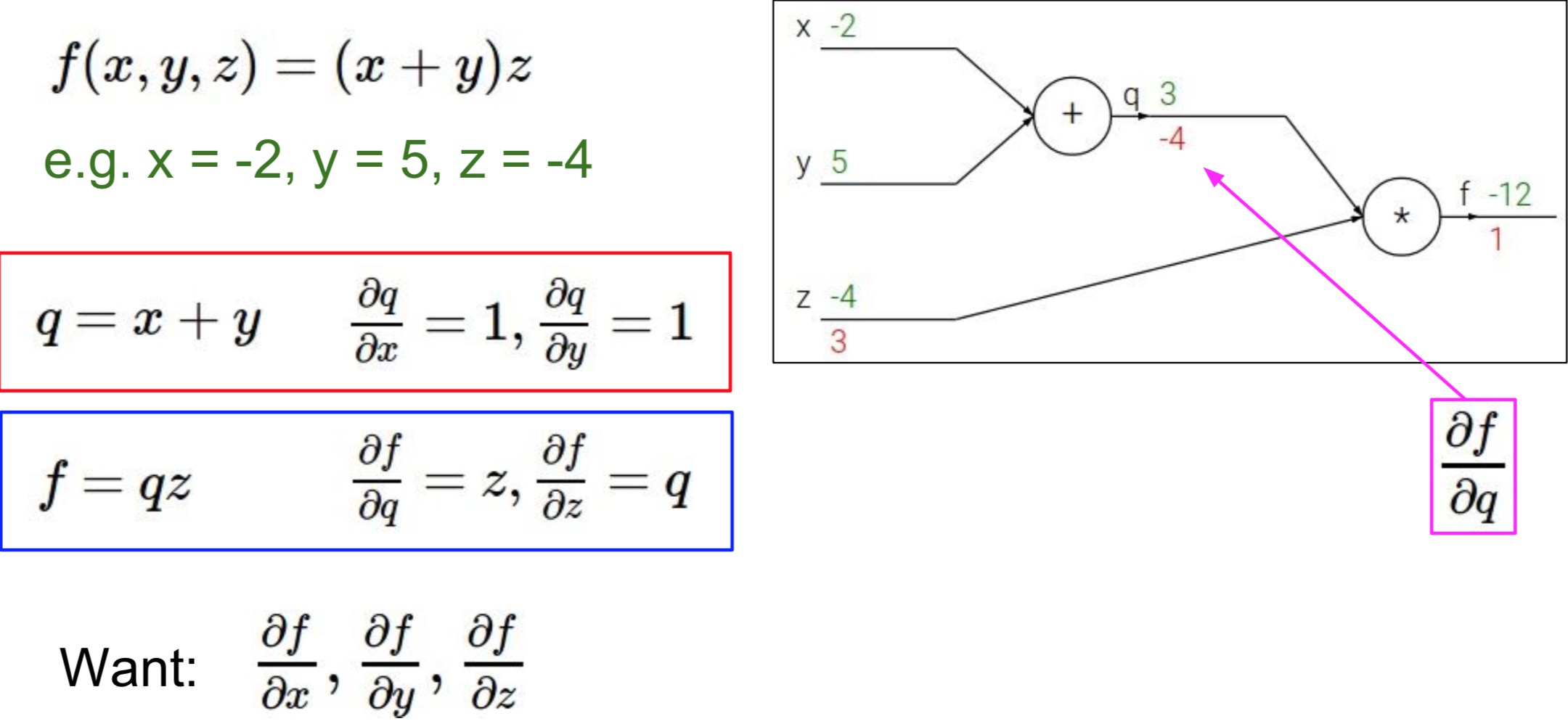
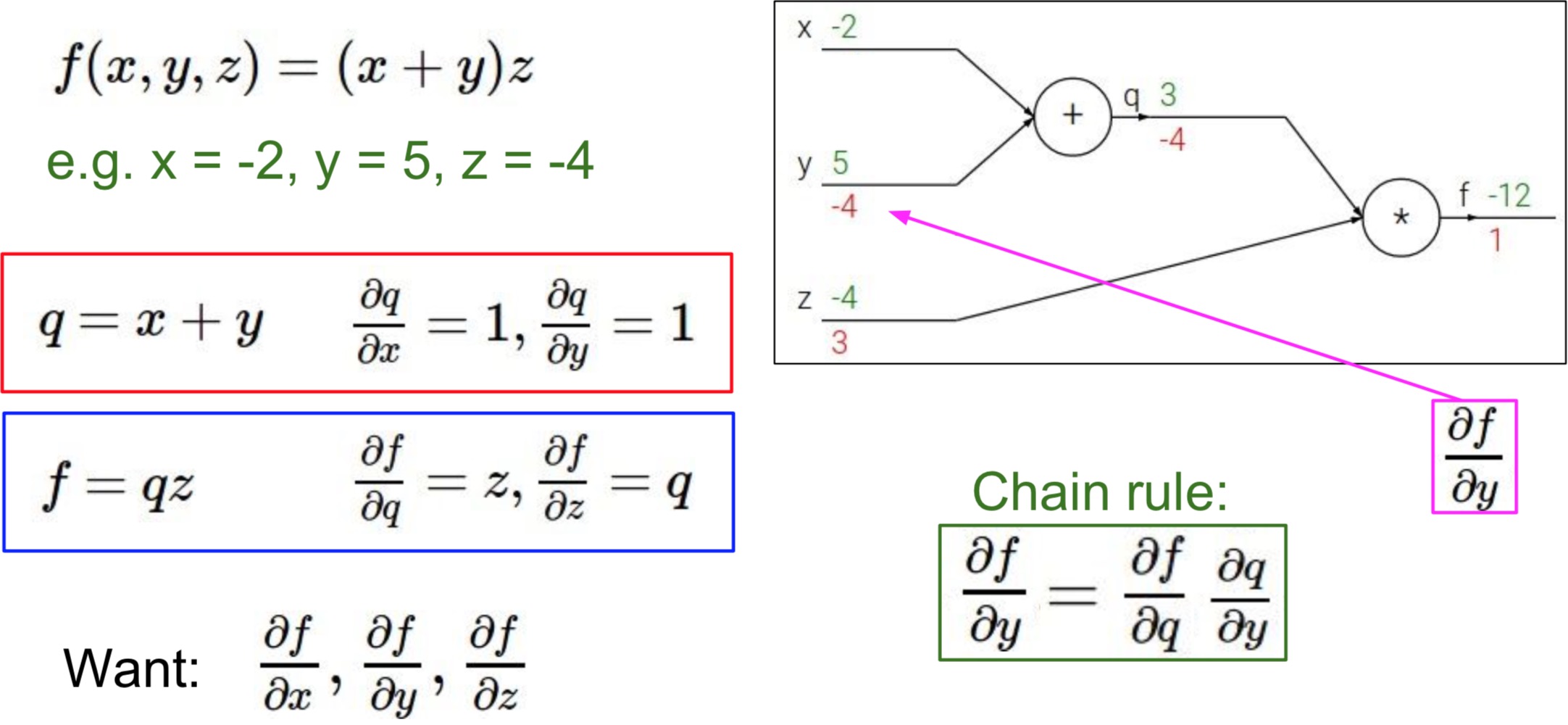
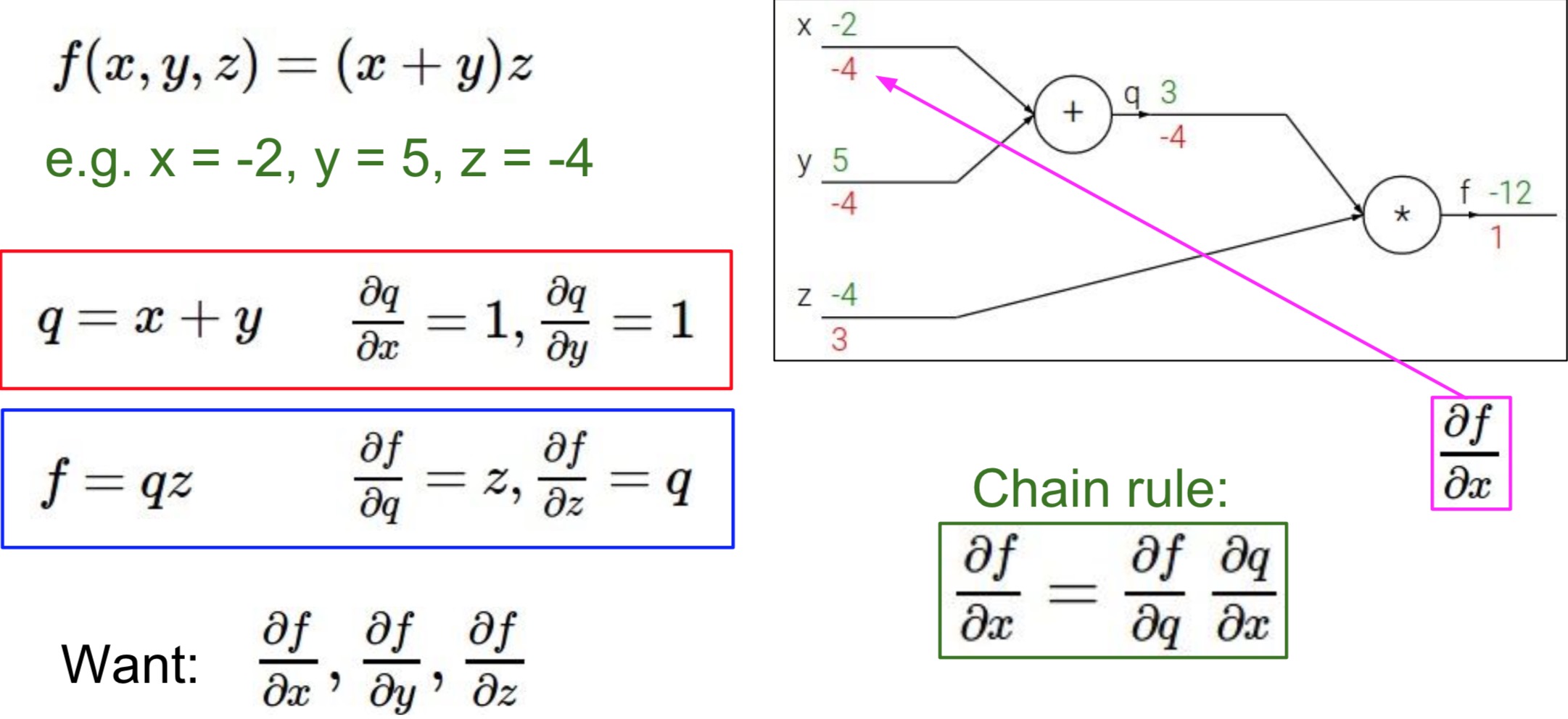
这一过程就是我们所说的反向传播的过程了。在反向传播的过程中,我们保留了一个个中间变量,即局部的梯度,这样我们继续反向求导的时候只需用链式法则直接乘以本级的导数即可,节省了大量的重复计算。
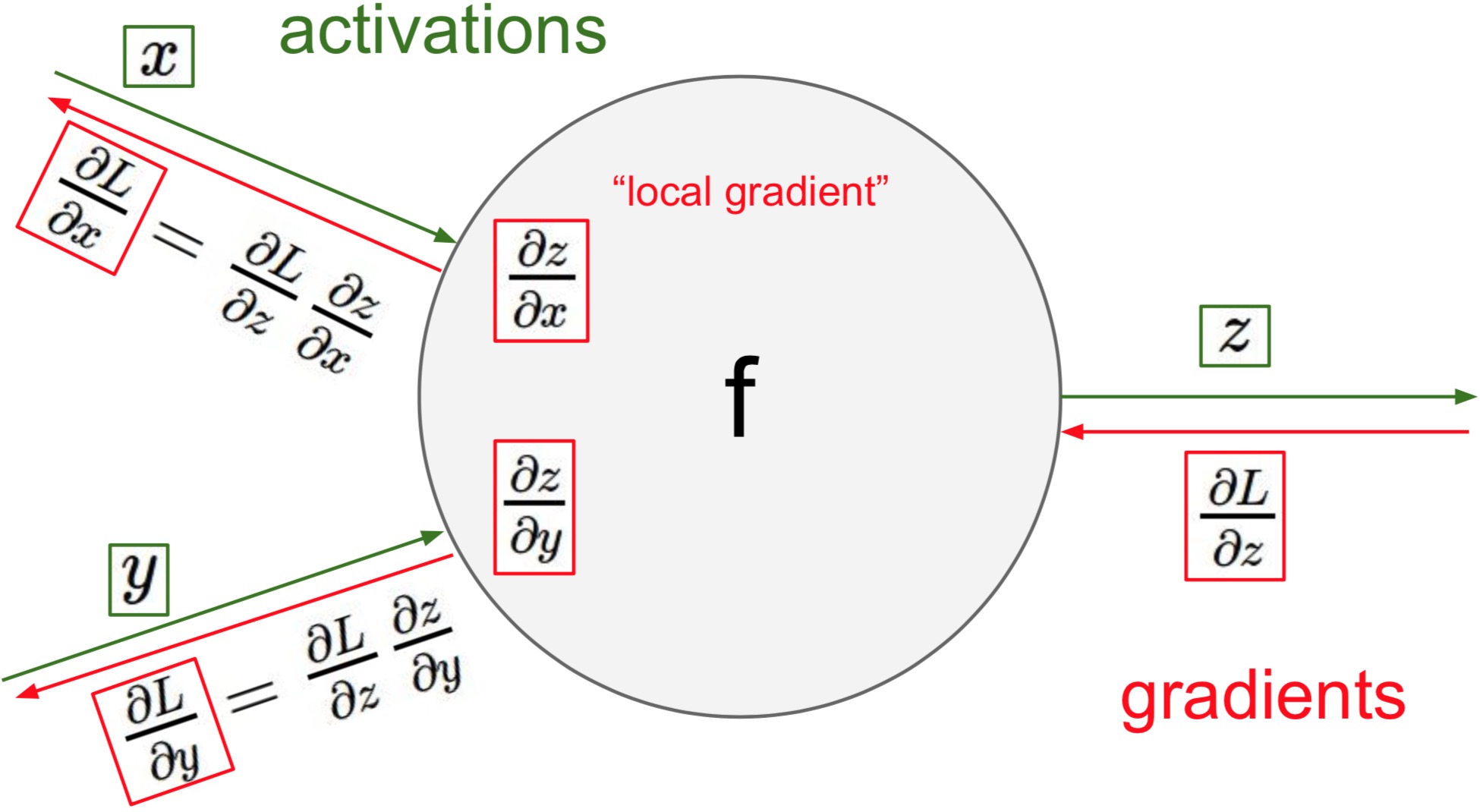
再放一个复杂点的例子,请自行跟着图片过一遍流程:
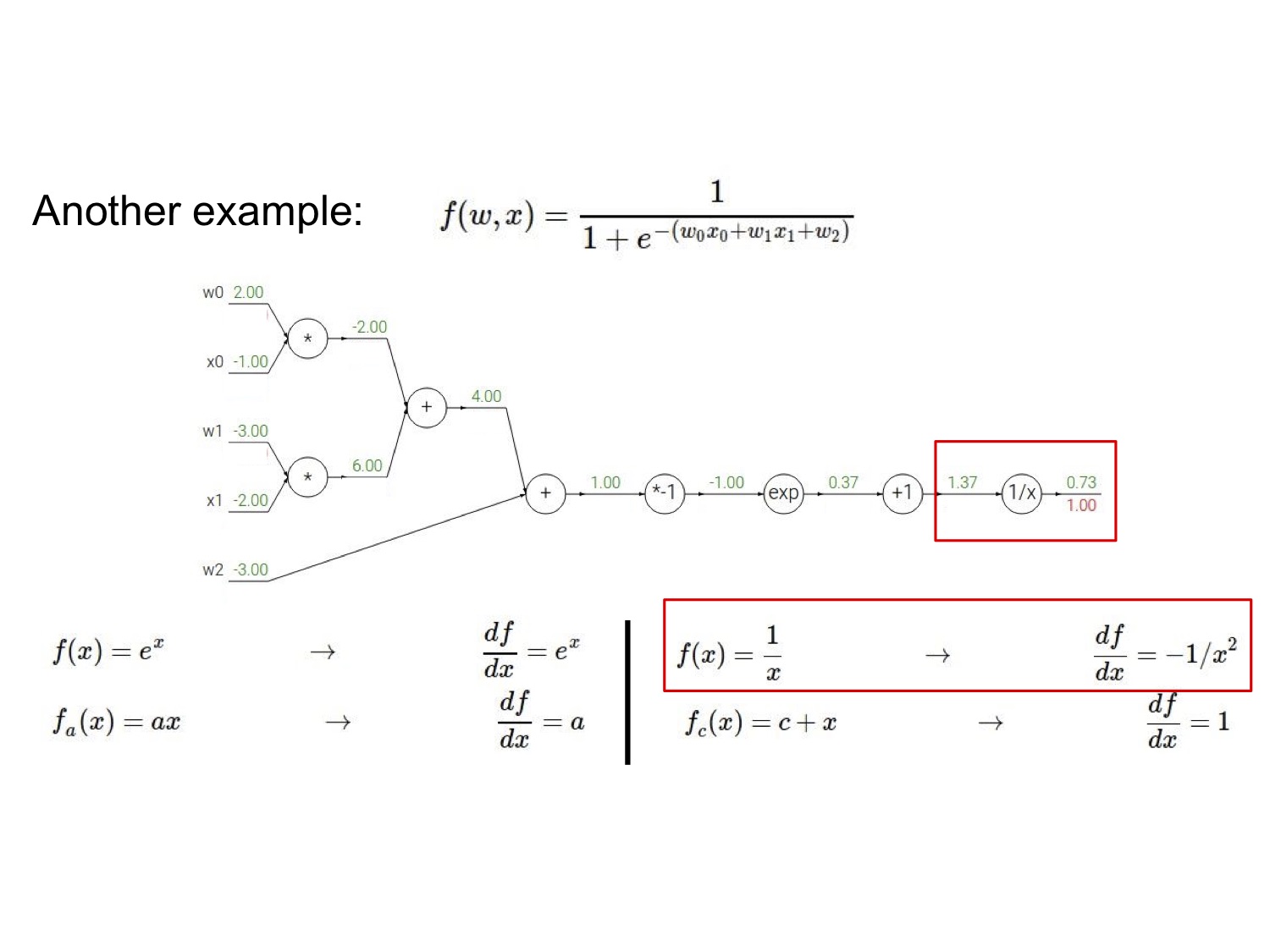
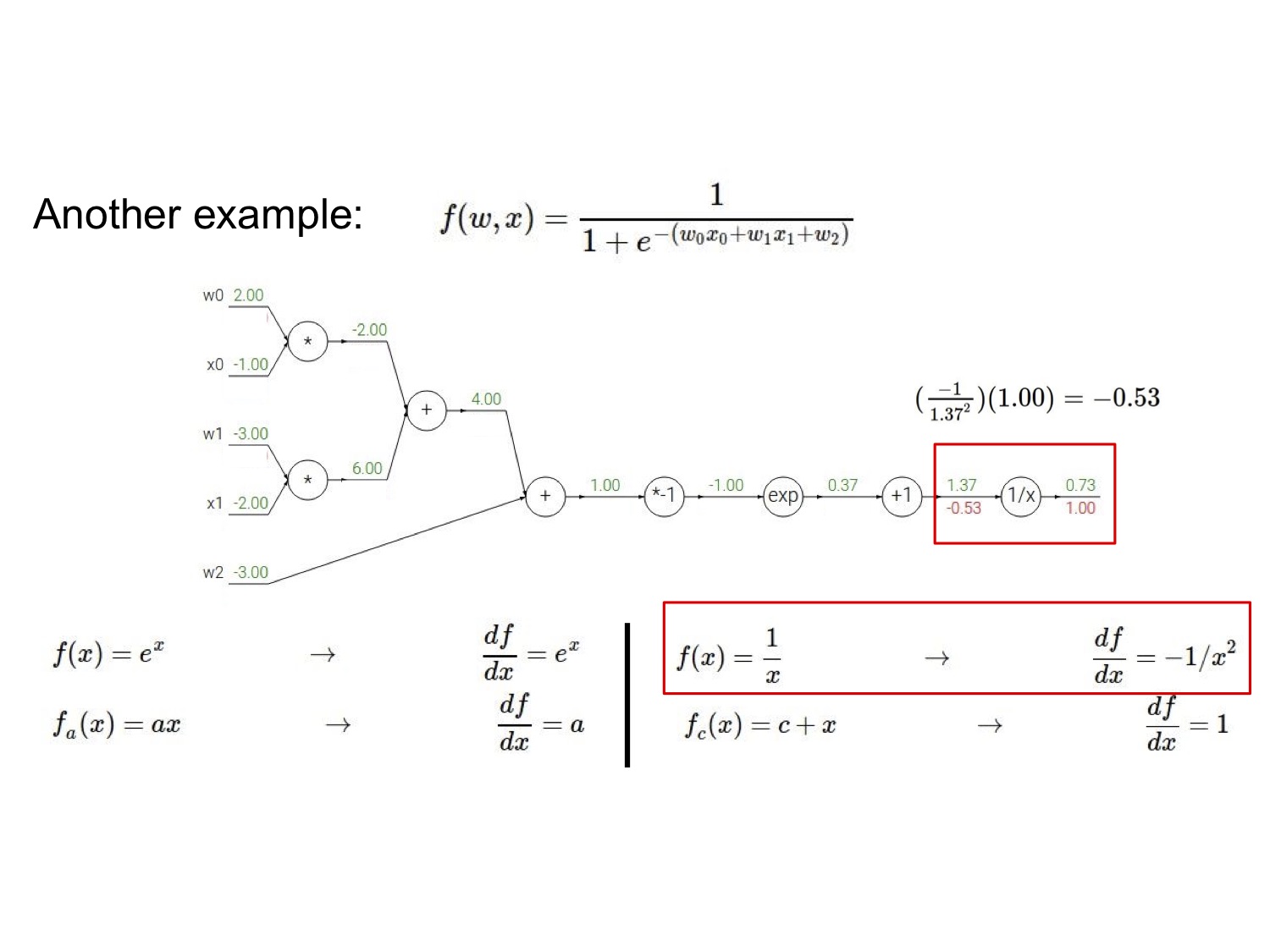
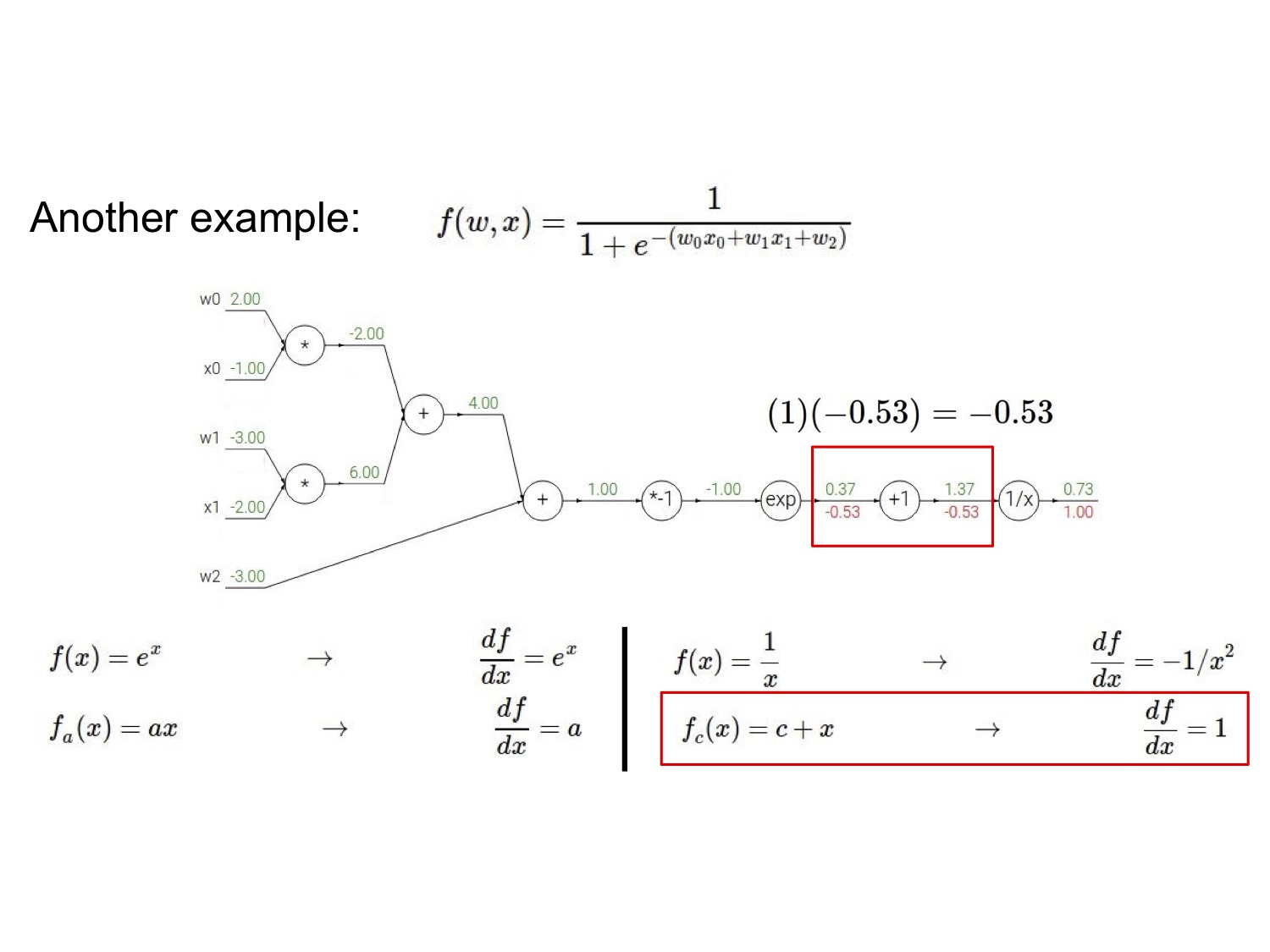
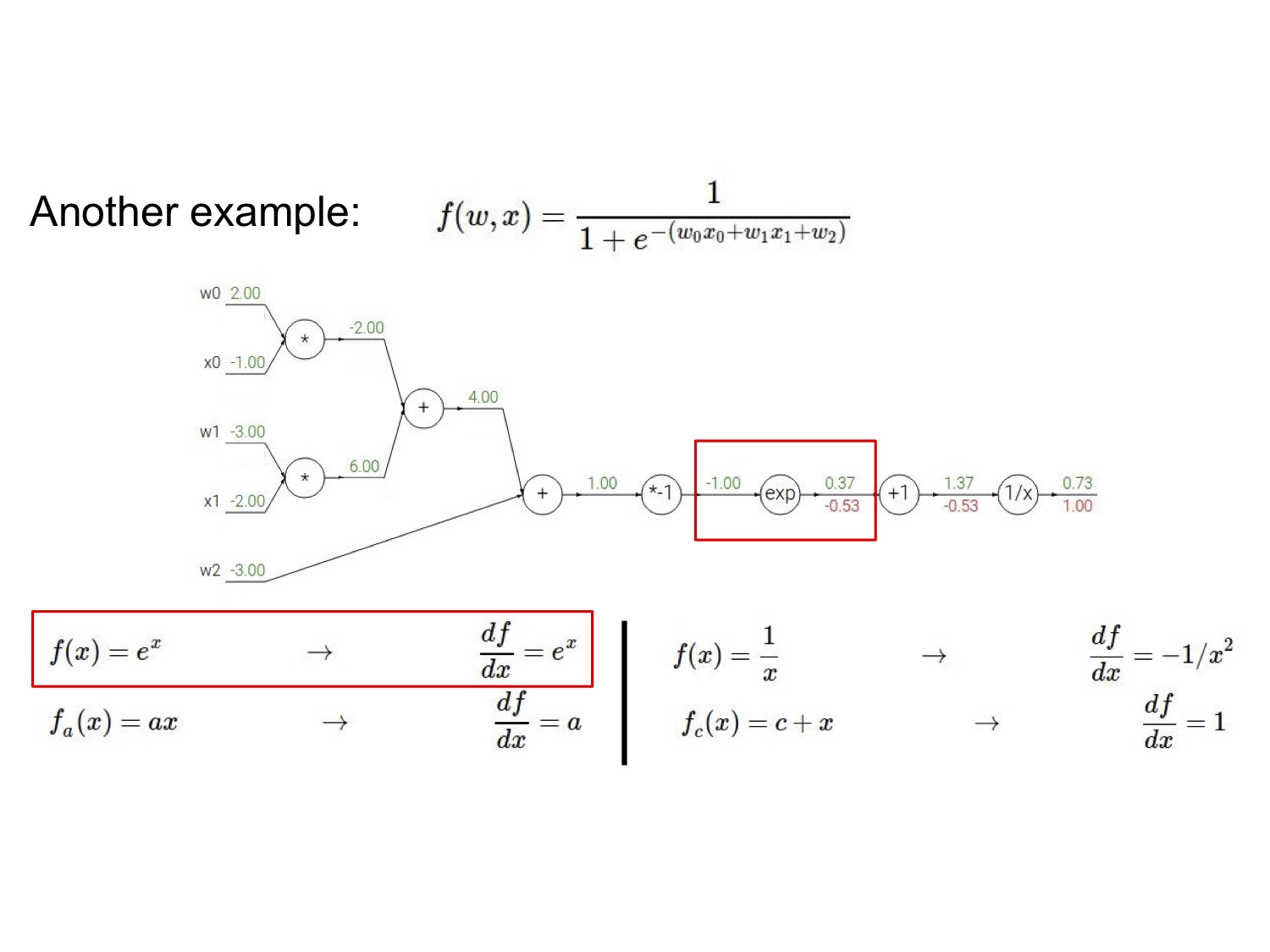
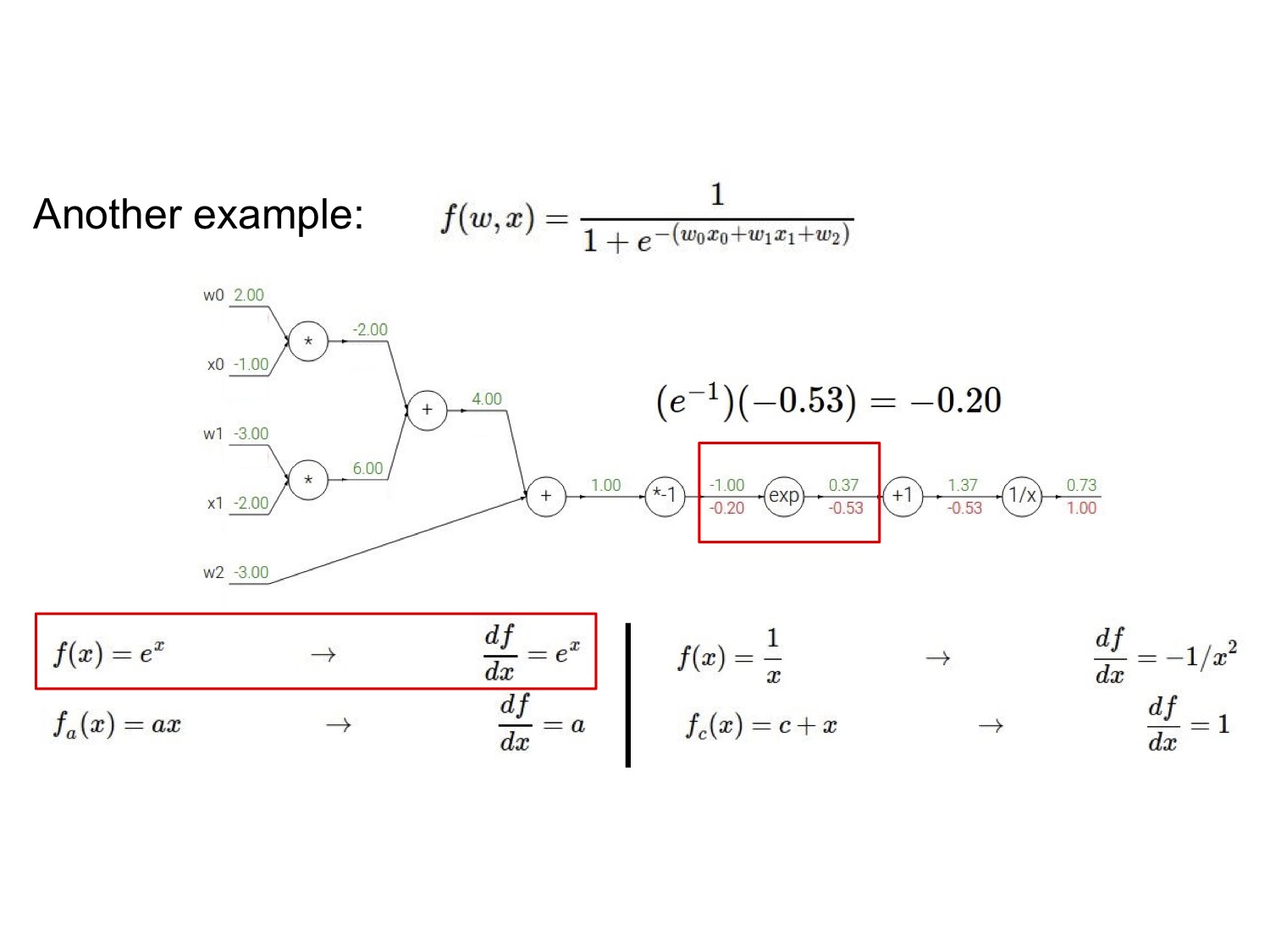

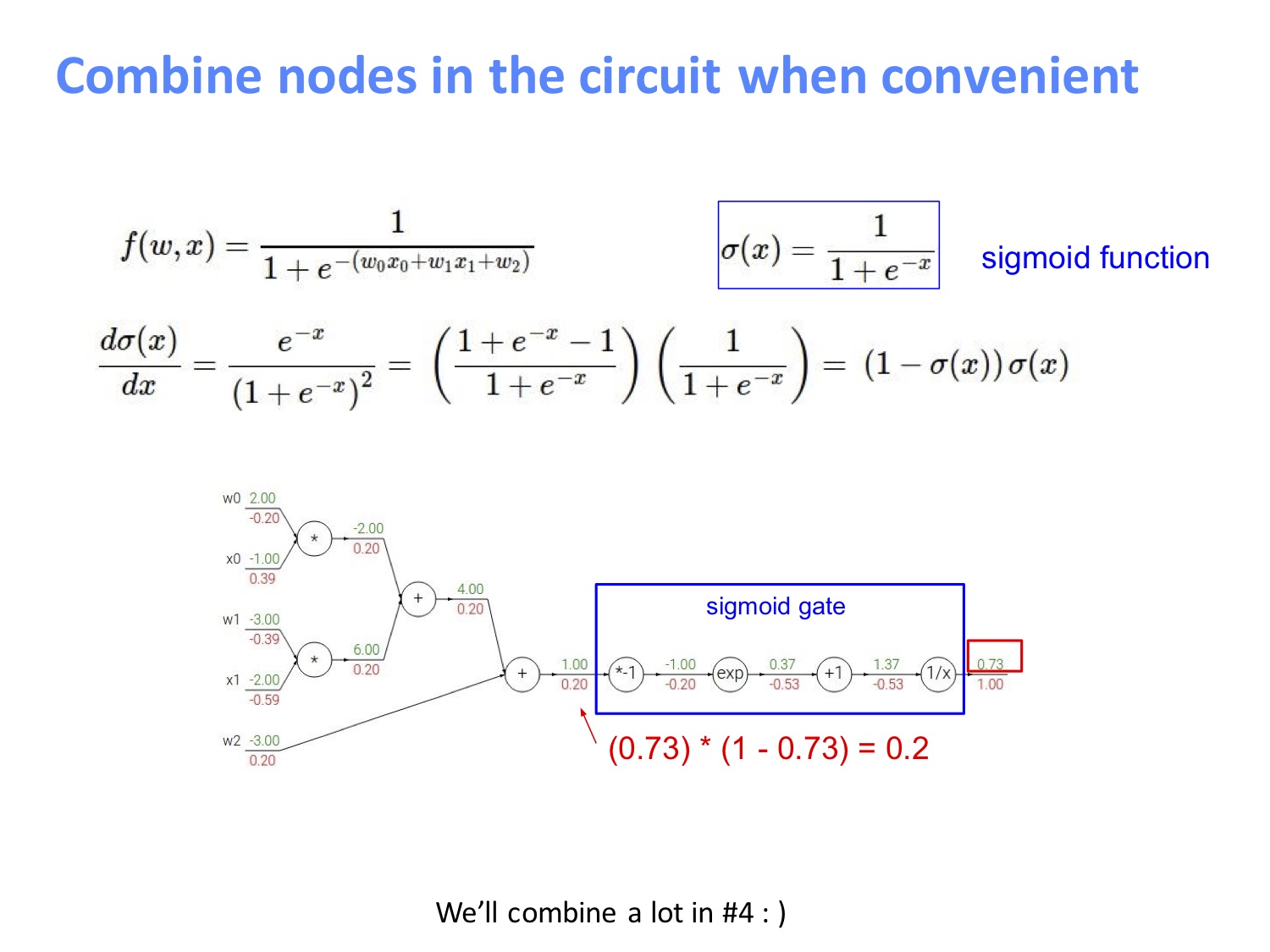
我们注意到电路图的右边其实是一个 sigmoid 门,由于 sigmoid 函数的导数形式很优雅:$\frac{d \sigma(x)}{dx}=\frac{\exp^{-x}}{(1+e^{-x})^2}=(\frac{1+e^{-x}-1}{1+e^{-x}})(\frac{1}{1+e^{-x}})=(1-\sigma(x))\sigma(x)$,因而可以简便地直接将后面几步合并起来带入计算。
流程图
流程图的解释方式也是很有意思的,我们可以将网络视为一个有向无环图来理解。
1条路径:
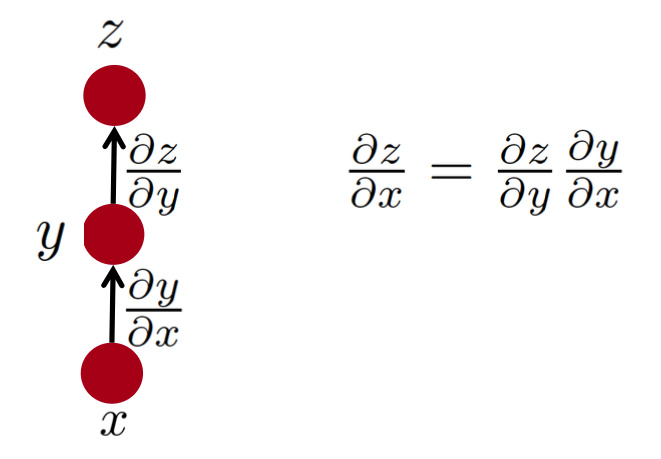
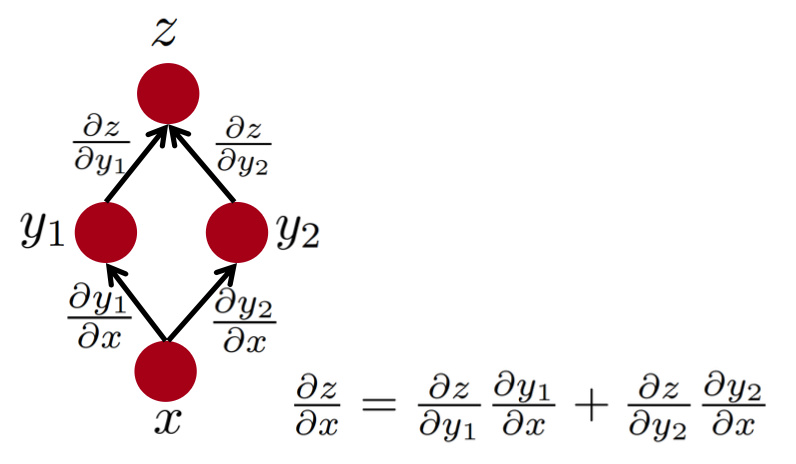
2条路径:
多条路径: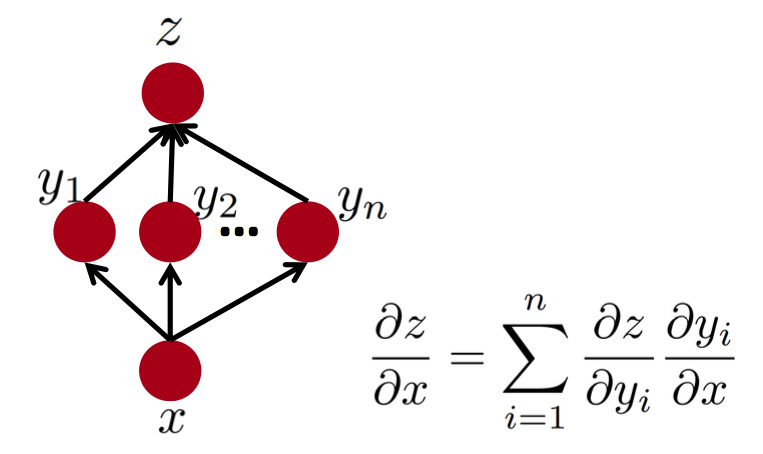
复杂的流程图:
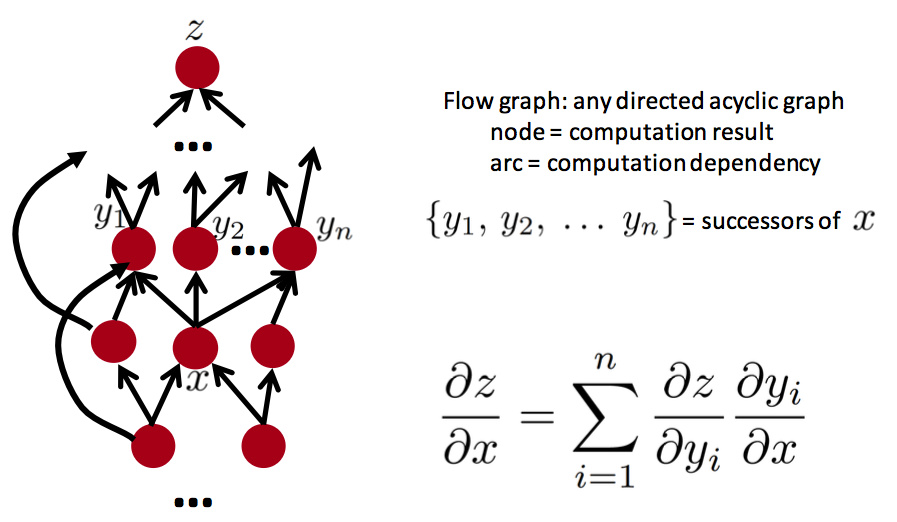
哪怕你带有激活函数,也是以一样的方式来进行反向地传递梯度,我们所需要做的就是先找出某个结点的各个父结点,然后再用链式法则并且求和:
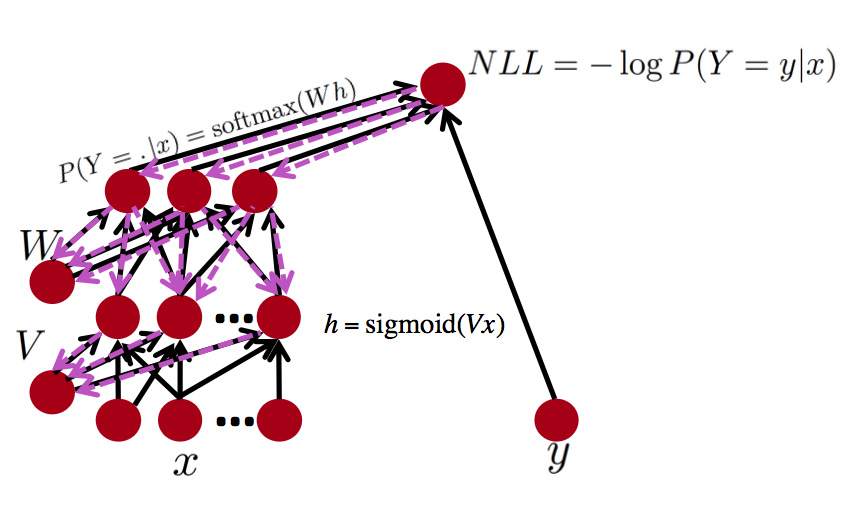
由这些图可以看出,其实对复杂网络进行反向传播计算还是挺麻烦的,所幸现在有一些软件包可以替我们完成这些计算。
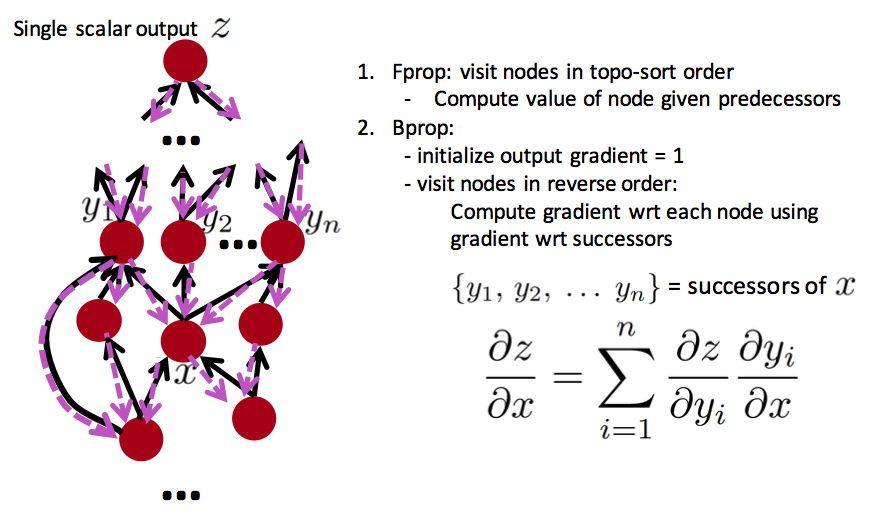
误差信号
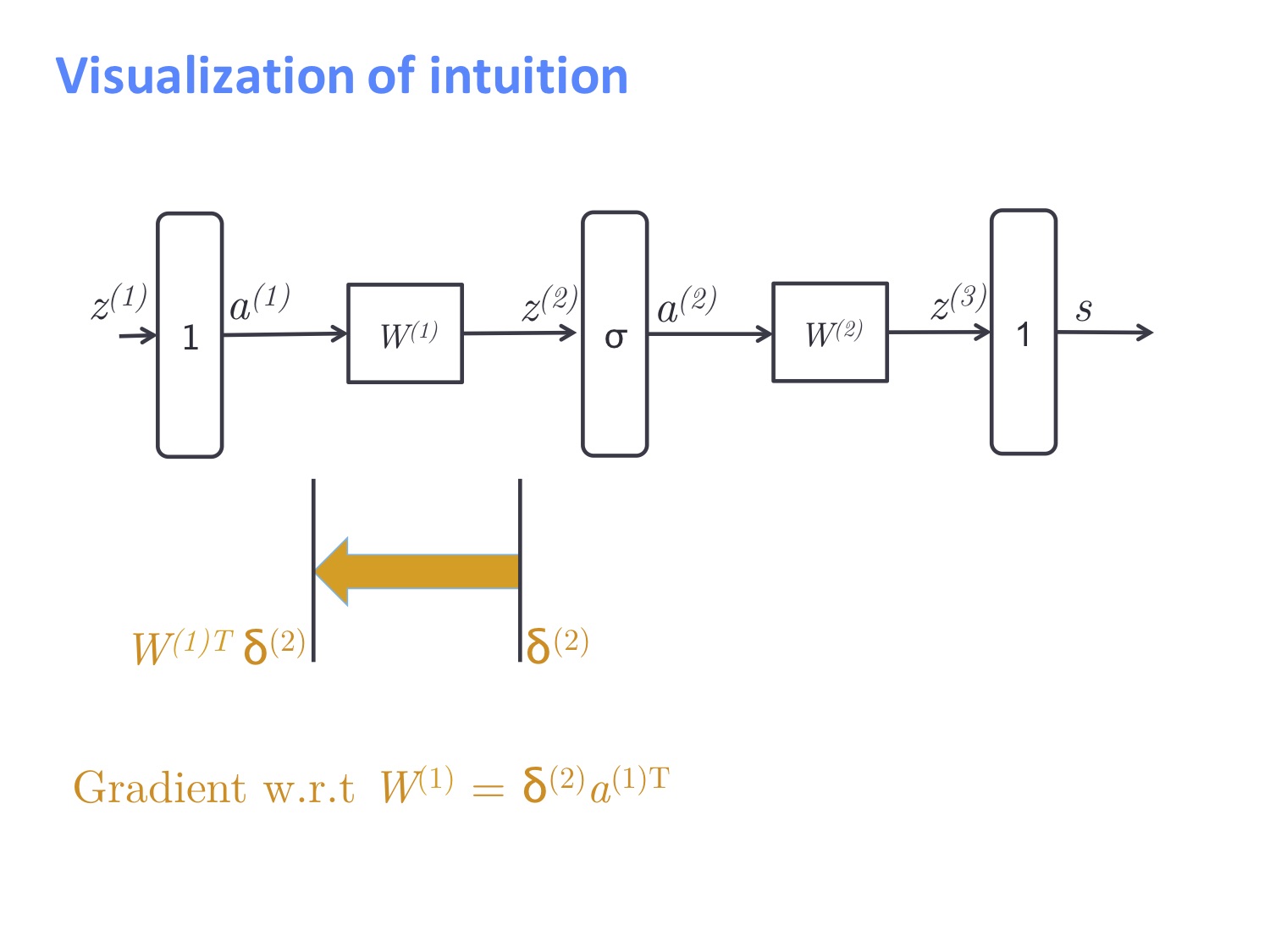
误差信号的传播这块举的是一个两层的神经网络为例:
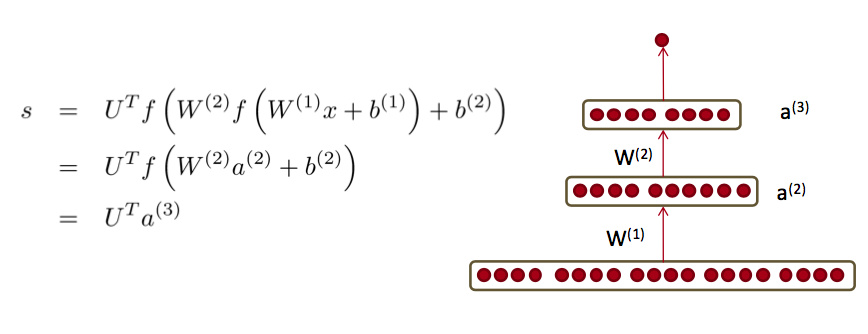
假设我们想要得到最初输入的导数,并且 $f=\sigma$ 则误差传播的流程如下所示,首先我们求的是最后一层对 $z^{(3)}$ 的误差 $\delta^{(3)}$:
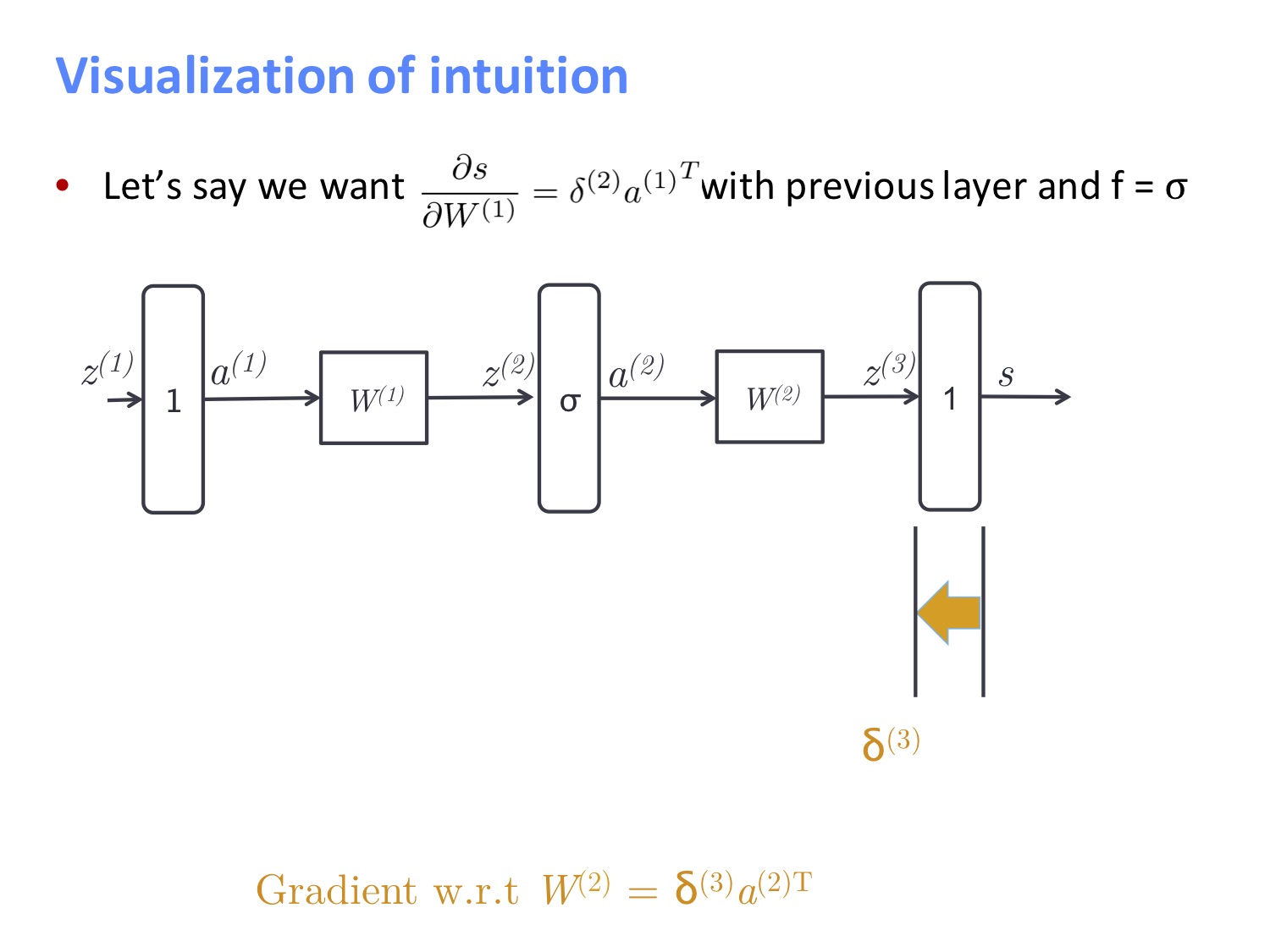
结合以下两图可以得知,对于线性层,我们直接做矩阵乘法即可,而对于非线性层,则是做逐元素相乘。我们可以知道 $W^{(2)}$ 的导数为 $\delta^{(3)}a^{(2)T}$。
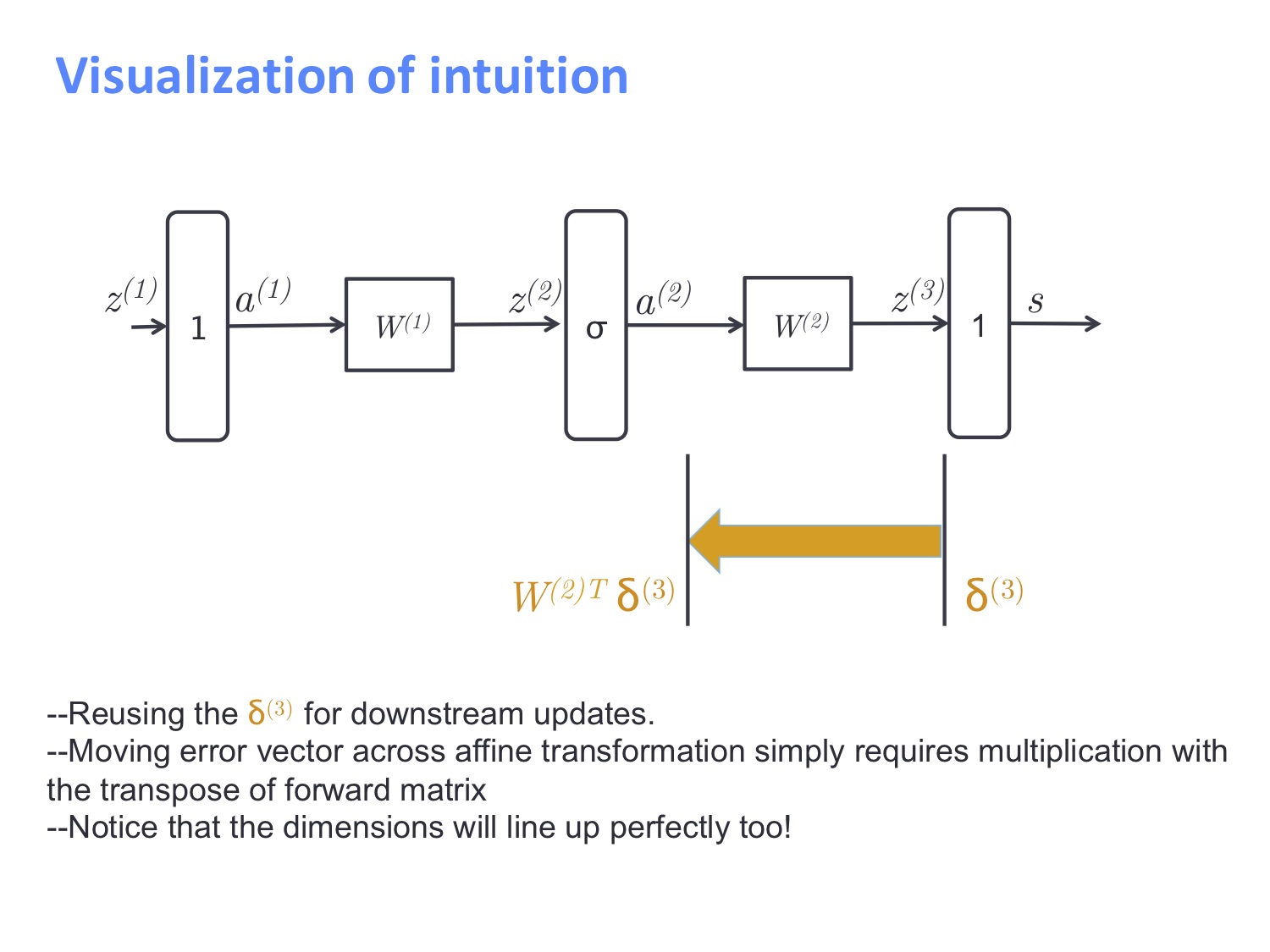
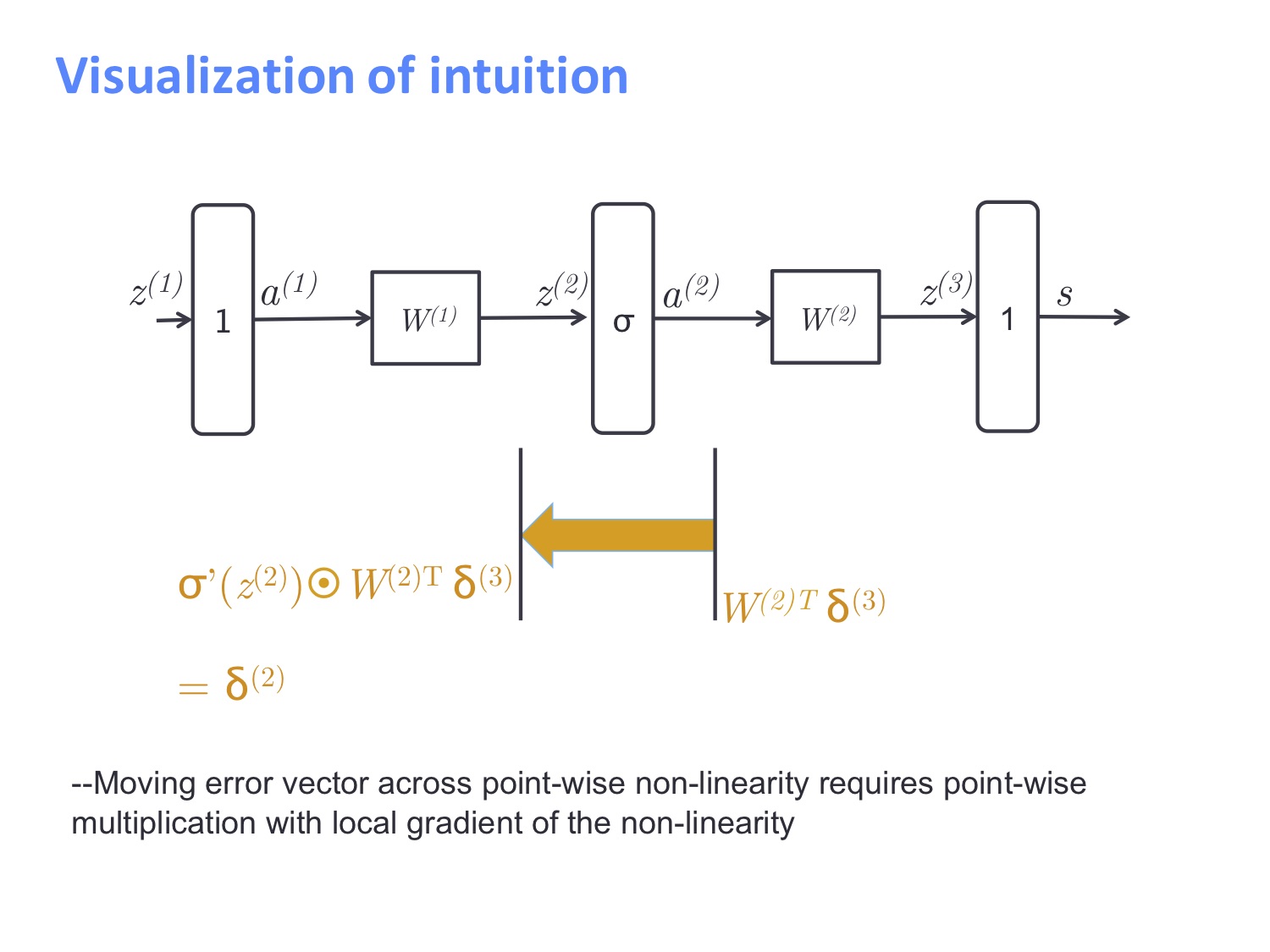
最终我们将误差信号从输出层传回了输入层,对于 $W^{(1)}$ 的导数为 $\delta^{(2)}a^{(1)T}$。
在经历 4 轮的轰炸之后,最终 Socher 小哥庆祝了一下大家还存活着。跟着课程过一遍 4 种角度的 BP 算法解读后,应该大家都能够对这个算法有所了解。
这里真的很想吐槽一下,某 A 厂的面试官,对面抛出了一个“你能解释一下 BP 神经网络和深度神经网络的区别吗?”的高难问题,我真的是一副被你打败了的表情,虽然在电话那头的你并不能看见。(手动微笑)
#课程项目的建议
这是对于这门课的 project 的建议,不过我认为还是蛮有道理的,姑且把几条建议给放出来:
- 明确你的任务
- 明确你的数据集
- 可以直接使用标准数据集
- 自己去搜集数据,但要注意别在抓取数据上花费太多时间,这样就本末倒置了
- 明确你的评估指标
- 划分数据集
- 建立起一个 baseline
- 先去实现一个最简单的模型,比如 LR。空中楼阁是不靠谱的,我们还是要脚踏实地一步一步地走
- 在训练集和开发集上计算评估指标
- 分析错误,这个是很重要的一点,先去了解 baseline 的不足之处,后续才能更好地改进模型
- 如果效果已经很好的话,那证明这个问题太简单了,没有挑战性,就可以省下一堆时间转做其他课题了
- 复现一下已有的网络模型
- 同样在训练集合开发集上计算评估指标
- 分析输出和错误
- 讲已有的模型作为本课程需要实现的最低标准
- [个人补充:将已有的模型扩展到新的领域上也是一种贡献,其实没必要整天就想着整个新模型出来,搞个大新闻]
- 确保一直围绕在数据左右
- 可视化数据集
- 搜集总结、统计
- 观察错误
- 分析不同参数下对性能的影响
- [个人补充:其实这里最重要的一点就是要确保自己的模型是由数据驱动的,一定要形成”数据驱动”的观念]
- 尝试修改模型,这时候可以考虑不同模型的优缺点,自行整合它们来达到目的


